|
Добрый день. Подскажите формулы при решении задачи на рис. 2.2 в лекции №2. Закон Ома, какие должны использоваться формулы для I и R |
Анализ деятельности офиса
Прогнозирование нестационарных показателей
Чаще всего среднее значение спроса с течением времени меняется. Такое изменяющееся среднее принято называть трендом. Для краткосрочного прогноза часто достаточно ограничиться линейным трендом. Наиболее распространены две модели линейного тренда. При линейно-аддитивном тренде среднее изменяется на постоянную величину за время dt. В линейно-мультипликативной модели тренд меняется на постоянный процент, например, ежемесячно спрос может возрастать на 2%. Рассмотрим подробнее линейно-аддитивную модель, когда спрос меняется в соответствии с формулой:
St = a + b* t + et
Здесь et - ошибка измерения. Если параметры модели a и b постоянны, их оценки можно получить по методу наименьших квадратов. Именно такие оценки реализованы в стандартных функциях Excel, предназначенных для прогнозирования. Однако можно рассматривать методы, когда предполагается, что и сами параметры меняются во времени. Метод, предложенный Холтом, использует ту же идею взвешенного суммирования, примененную в экспоненциальном сглаживании. Вот соотношения для расчета оценки прогноза и оценки параметра b:

Здесь dt - временной интервал между двумя последними измерениями. Прогнозируемое значение на момент времени t+t1 вычисляется по формуле:
Ft + t1 = Pt + bt * t1
Некоторым недостатком метода является необходимость эмпирического задания двух констант  и
и 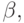 задающих веса. В методе двойного сглаживания Брауна достаточно ввести одну константу. Прогнозируемое значение здесь вычисляется по формуле:
задающих веса. В методе двойного сглаживания Брауна достаточно ввести одну константу. Прогнозируемое значение здесь вычисляется по формуле:
Ft + t1 = 2Pt - Qt + bt * t1
Двойное экспоненциально взвешенное среднее вычисляется из соотношения:
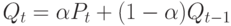
Оценка коэффициента bt дается формулой:
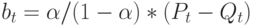
Есть и другие модели краткосрочного прогнозирования тренда, например, методы Бокса-Дженкинса.
Сезонный спрос
Сезонные колебания действуют независимо от других факторов и накладываются на ту или иную модель спроса. Проще всего учесть сезонный фактор, используя коэффициенты сезонности. Так, если, как обычно, принять сезонный цикл за год, можно иметь 52 недельных или 12 месячных коэффициентов сезонного спроса. Коэффициент сезонности представляет собой отношение среднего спроса за текущий период ( месяц) к среднему значению за весь период цикла (год). Чтобы оценить значения коэффициентов сезонности, требуются данные за несколько лет. Достоверность результатов обычно можно повысить за счет того, что сезонные циклы одинаковы для разных товаров.
Если сезонные коэффициенты рассчитаны, то учет сезонности не вызывает трудностей для любой из моделей тренда. Вначале необходимо текущие значения очистить от влияния сезонности делением на соответствующий коэффициент. Затем применить обычный алгоритм прогноза и полученную прогнозную оценку умножить на коэффициент сезонности, соответствующий моменту прогноза.
Среднесрочный прогноз и методы регрессионного анализа
Для среднесрочного прогноза обычно применяются методы регрессионного анализа. Хотя ничто не мешает применять их и для краткосрочного прогноза. Они основаны на получении оценок по методу наименьших квадратов. Эти методы и реализованы в стандартных функциях Excel, так что рассмотрим их подробнее. Начнем с наиболее простой модели линейного тренда. В основе модели лежит уже упоминавшееся соотношение:
Yt = a + b* t + Et
Это соотношение можно интерпретировать следующим образом. В каждый момент времени t измеренное значение спроса Yt является суммой неизвестной помехи Et и линейной функции времени с неизвестными (ненаблюдаемыми) параметрами a и b. Из-за помех решения, принимаемые на основе измерений, носят вероятностный характер. Найти точные значения параметров a и b в этих условиях невозможно, но, зная выборку Yt, можно вычислить оценки параметров. В статистике оценкой называют любую функцию от измерений. Оценки параметров a и b можно получить по методу наименьших квадратов из условия минимизации квадратичного функционала:
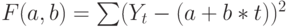
При этом, когда мы имеем дело с линейной моделью, минимум этого функционала находится аналитически, и в случае двух параметров можно явно выписать конечные соотношения для оценок параметров a и b. В этом одно из преимуществ метода наименьших квадратов. Прямая Yt = в + ^b* t, где a и ^b - оценки параметров, называется линией регрессии и используется для прогнозирования значений Y в произвольные моменты времени t. Конечно, чем дальше отстоит значение t от интервала наблюдений, тем вероятнее, что ошибка прогноза будет увеличиваться.
Метод наименьших квадратов хорош и с точки зрения статистики. Если предположить, что неизвестные нам помехи распределены по нормальному закону с нулевым математическим ожиданием и, в общем случае, с заданной корреляционной матрицей, то полученные оценки обладают важными свойствами несмещенности, состоятельности и эффективности. Мы не будем давать строгого определения всех этих терминов. Скажем лишь, что в классе несмещенных оценок наши оценки обладают минимальной дисперсией, т. е. минимальным разбросом относительно истинного значения параметров. Чем больше измерений, тем точнее оценки, так как уменьшается интервал, накрывающий истинное значение параметра с заданной вероятностью. Как ни странно, но практика показала, что предположения о характере помех зачастую оправдываются. В теории вероятностей этому факту есть хорошее объяснение. Недаром открытый Гауссом закон распределения называется "нормальным". Все в нашей жизни распределено по гауссиане.
Обобщим теперь постановку задачи на произвольное количество параметров, полагая теперь, что спрос может быть описан уже не линейной, а полиномиальной функцией времени, например:
Yt = a0 + a1 t + a2t2 + … + amtm + Et
Это полиномиальное относительно времени соотношение остается линейным по отношению к неизвестным параметрам. Для простоты перейдем к матричной форме записи соотношений:
Y = X*a + E
Здесь Y - вектор измерений, a - вектор параметров, E - вектор ошибок, X - прямоугольная матрица, элементы которой зависят от t и не зависят от параметров a. Для полиномиальной зависимости нетрудно выписать явный вид ее элементов:
X = || ti j.|| i= 1…n; j = 0..m;
Число строк этой матрицы определяется моментами времени t1, t2, … tn, в которые производились измерения, а количество столбцов определяется степенью полинома. Квадратичный функционал F(a) в матричной форме имеет вид:
F(a) = (Y - X*a)T R-1 (Y - X*a)
Продолжая обобщать постановку задачи, мы ввели корреляционную матрицу R ошибок измерений. В частном случае, когда отсутствует корреляция ошибок измерений и дисперсия их единична, матрица R превращается в единичную матрицу. Другой важный частный случай - диагональный, когда корреляция отсутствует, но дисперсия ошибки меняется от измерения к измерению. Величину, обратную к дисперсии 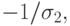 можно рассматривать как вес измерения. Так что введение этой матрицы позволяет приписать разный вес измерениям, придавая, например, больший вес последним измерениям.
можно рассматривать как вес измерения. Так что введение этой матрицы позволяет приписать разный вес измерениям, придавая, например, больший вес последним измерениям.
Все эти обобщения не нарушают возможности получения аналитического решения. Вектор оценок a, минимизирующий квадратичный функционал F(a), определяется по формуле:
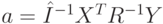
Здесь 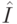 - информационная матрица Фишера, вычисляемая из соотношения:
- информационная матрица Фишера, вычисляемая из соотношения:
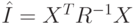
Наряду с вектором оценок нетрудно получить и его статистические характеристики. Поскольку оценки являются несмещенными, для полного знания распределения вектора оценок достаточно знать его корреляционную матрицу. В данном случае она является обратной к матрице Фишера.

Даже если исходные измерения независимы, между оценками параметров может возникать корреляция. Правда, на практике чаще всего используют только значения их дисперсий.
До сих пор мы рассматривали временные ряды, и в наших измерениях присутствовал только один наблюдаемый параметр - время. В регрессионном анализе обычной ситуацией является проведение измерений, когда в каждой точке фиксируется несколько наблюдаемых параметров, влияющих на измеряемое значение. Применительно к задаче спроса такими параметрами могут быть, например, уровень текущей рекламы, количество конкурирующих товаров, погодные условия. Так что линейная относительно неизвестных параметров модель спроса в общем случае может быть такой:
Yi = a0 + a1 x1i + a2x2i+ … + amxmi + Ei
В матричной форме записи все соотношения остаются справедливыми, изменяются лишь соотношения для расчета элементов матрицы X. В заключение отметим, что при долговременном прогнозировании предположение о линейности тренда вряд ли справедливо, кривая спроса имеет более сложную форму и не описывается линейной функцией относительно параметров. В этом случае определить аналитически точку минимума квадратичного функционала F(a), обычно уже невозможно. Правда, есть одно важное исключение. Пусть:
Yi = F(a0 + a1 x1i + a2x2i+ … + amxmI)+ Ei
и функция G является функцией, обратной к F. Тогда линейная модель по-прежнему имеет место, но уже для преобразованных значений измерений:
G(YI )= (a0 + a1 x1i + a2x2i+ … + amxmI)+ Ei
С точки зрения статистики это преобразование измерений нарушает предположение о нормальном характере поведения измерений. Если закон распределения Yi был нормальным, то закон распределения G(Yi) таковым уже не будет. Поэтому найденные оценки лишаются теоретически обоснованного хорошего качества их поведения. На практике же такие процедуры применяют часто.
Но вовсе не обязательно приводить нашу модель к линейной относительно параметров. Она спокойно может оставаться нелинейной, так как существуют хорошо разработанные численные методы. Более того, можно использовать для минимизации функционала средство самого Excel - Решатель. Думается, найти минимум функционала не столь сложно - сложнее построить адекватную реальной ситуации модель спроса. Здесь надо выяснить, какие параметры, влияющие на спрос, поддаются прямому наблюдению, а какие требуется оценить по результатам наблюдений. Не менее сложно подобрать аналитическое описание кривой спроса с точностью до неизвестных параметров. Таким образом, экономисту, математику и программисту есть где поработать, создавая эффективную систему прогноза. Средства Office 2000, прежде всего Excel, облегчают решение этой задачи, а нередко позволяют получить ее решение на основе встроенных стандартных функций.
Встроенные функции Excel и прогнозирование
Для решения задач прогнозирования в Excel встроены несколько функций. По существу все они сводятся к нахождению оценок по методу наименьших квадратов в задаче линейной регрессии. Наряду с оценками вычисляются и их статистические характеристики, что позволяет строить доверительные интервалы и делать выводы, имеющие вероятностный характер.
Функция ЛИНЕЙН
В общем случае решает задачу линейной множественной регрессии, вычисляя по методу наименьших квадратов вектор оценок параметров. Используется описанная нами выше модель:
Y = X*a + E
Синтаксис вызова этой функции:
ЛИНЕЙН (Известные_значения_Y; Известные_значения_X; Конст; Статистика)
Параметры функции имеют следующий смысл:
- Известные_значения_Y - задает вектор измерений.
- Известные_значения_X - в общем случае матрица значений наблюдаемых параметров. Если речь идет о временном тренде, то элементы X задают моменты времени, в которые проводились измерения. Можно опустить X, если значения элементов составляют последовательность 1, 2, 3 и т. д.
- Булев параметр " Конст " равен Истина (True), если в линейной записи модели присутствует дополнительно свободный член b, не входящий в вектор параметров a.
- Булев параметр " Статистика " равен Истина (True), если наряду с оценками параметров вычисляются и статистические характеристики.
- Результат вычислений этой функции - массив, в общем случае состоящий из 5 строк и n+1 столбцов, где n - это размерность вектора искомых параметров a.
- an, an-1, … a1, b
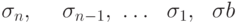
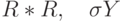
- F, df
- Ssreg, Ssresid
- В первой строке идут оценки параметров a и свободного члена b. Оценки идут в обратном порядке, начиная с an. Они и определяют линию регрессии, позволяя рассчитать прогнозируемое значение Y в любой точке, где заданы значения наблюдаемых параметров.
- В следующей строке идут среднеквадратические отклонения этих оценок. Выше мы показали, как вычислить полную корреляционную матрицу оценок. Среднеквадратические отклонения являются диагональными элементами этой матрицы. Точнее, на диагонали стоят их квадраты - дисперсии
 . Значения
. Значения 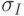 позволяют построить доверительный интервал для соответствующих оценок и вынести суждение об их значимости в линейной модели. Как вычисляются эти значения в Excel, нам осталось непонятно, так как алгоритм не описан. Можно лишь заметить, что применяемый алгоритм не всегда корректен с позиций классической математической статистики. Приведем пример. Пусть оцениваются, как часто бывает, два параметра a и b (Y = at +b). Пусть выполнены всего два измерения - Y1 и Y2. Тогда, каковы ни были ошибки в измерениях, линия регрессии пройдет через две наблюденные точки. Excel скажет, что оши
"µ
бок в оценках параметров нет, и выдаст значения
позволяют построить доверительный интервал для соответствующих оценок и вынести суждение об их значимости в линейной модели. Как вычисляются эти значения в Excel, нам осталось непонятно, так как алгоритм не описан. Можно лишь заметить, что применяемый алгоритм не всегда корректен с позиций классической математической статистики. Приведем пример. Пусть оцениваются, как часто бывает, два параметра a и b (Y = at +b). Пусть выполнены всего два измерения - Y1 и Y2. Тогда, каковы ни были ошибки в измерениях, линия регрессии пройдет через две наблюденные точки. Excel скажет, что оши
"µ
бок в оценках параметров нет, и выдаст значения 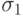 и
и 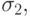 равные 0, хотя ясно, что это не так.
равные 0, хотя ясно, что это не так. - Коэффициент детерминации R2 имеет значение в интервале от 0 до 1 и позволяет оценить, насколько хорошо сглаживаются измеренные значения линией регрессии. Он равен 1, если линия регрессии проходит через все измеренные точки. При этом можно полагать, что есть строгая функциональная зависимость между измеряемым значением Y и параметрами ai. Предыдущий пример показывает, что недостаточное количество измерений может приводить к такому же результату. Поэтому и к этому параметру надо относиться с осторожностью. Вычисляется коэффициент детерминации по формуле:
R2 = Dreg / D
и представляет отношение дисперсии, объясняемой регрессией, к общей дисперсии. О смысле этих терминов мы скажем чуть ниже.
- Мы и так увлеклись понятиями математической статистики, потому не будем говорить о том, что означают и как используются параметры
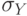 , F и число степеней свободы df.
, F и число степеней свободы df. - Последние два значения - Ssreg и Ssresid задают дисперсию, объясняемую регрессией, и остаточную дисперсию, представляющую разность между общей дисперсией и Dreg. Обе дисперсии вычисляются "обычным" способом:
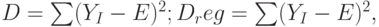
где E - среднее значение измеренных значений, а YI - сглаженные значения, вычисленные из уравнения регрессии.
Мы подробно рассказали о "главной" для решения задач прогнозирования функции ЛИНЕЙН. Она позволяет построить уравнение регрессии, как для временных рядов, так и в общем случае линейной множественной регрессии, когда наблюдается несколько параметров.
