|
"Теоретически канал с адресацией EUI 64 может соединить порядка запись вида ее можно заменить например на записи вида 264 или 1,8 * 1019
|
Адресация IPv6
Длина адреса IPv6
— Скажите, Шура, честно, сколько вам нужно денег для счастья? — спросил Остап. — Только подсчитайте все.
— Сто рублей, — ответил Балаганов, с сожалением отрываясь от хлеба с колбасой.
— Да нет, вы меня не поняли. Не на сегодняшний день, а вообще. Для счастья. Ясно? Чтобы вам было хорошо на свете.
Балаганов долго думал, несмело улыбаясь, и, наконец, объявил, что для полного счастья ему нужно шесть тысяч четыреста рублей и что с этой суммой ему будет на свете очень хорошо.
— Ладно, — сказал Остап, — получите пятьдесят тысяч.
(И. Ильф, Е. Петров. "Золотой теленок")
Наша задача номер один — расширить адресное пространство. Поэтому начнем мы нашу "революцию в IP", конечно же, с сетевого адреса. А самый первый вопрос касательно нового адреса звучит предельно просто: сколько адресных битов будет достаточно, чтобы избежать в обозримом будущем новых "революций"? Вариантов ответа на этот вопрос есть немало, однако почти все их можно отнести к одной из трех больших групп:
- "не надо гадать на кофейной гуще": оставим попытки предсказать длину нового адреса IP и сделаем ее переменной;
- "к природе за советом": давайте посмотрим, сколько всего песчинок в пустыне Сахара, молекул воды в мировом океане или протонов в наблюдаемой вселенной, и решим, что большего числа адресов IP человечеству никогда не понадобится;
- "возможности во главе угла": длина адреса IP должна стать такой, чтобы это открыло новые возможности на уровне работы протокола.
Первый подход, безусловно, очень хорош в теории, так как он позволил бы просто увеличивать длину адреса по мере расходования адресного пространства. Более того, он не нов и применяется в протоколе ISO CLNP. С другой стороны, адреса переменной длины значительно труднее обрабатывать аппаратно. Вдобавок, длина сетевого заголовка тоже становится переменной, а это еще сильнее затрудняет быструю аппаратную обработку пакетов. Так как IP уже давно применяют в областях, где требования к скорости обработки пакетов очень высоки (телефонные магистрали, системы управления реального времени), нам придется отказаться от этого подхода, несмотря на его привлекательность.
Кстати, и интегральные схемы, и программы для работы с адресами переменной длины стали бы не только сложнее, но и дороже. Учитывая, что скоро стек TCP/IP будет встроен буквально в каждую кофеварку, фактор стоимости тоже играет большую роль.
Тем не менее, любопытно отметить, что эта простая идея: "TCP и UDP поверх ISO CLNP", — легла в основу одной из альтернативных разработок "IP нового поколения", известной как TUBA [RFC 1347]. Это было изящно, не правда ли? Если бы проект TUBA удался, мы бы с вами сейчас "разрабатывали" IPv9 вместо IPv67 http://www.iana.org/assignments/version-numbers . Однако даже сами авторы TUBA выражали опасение, что гибкость адресации CLNP будет в ущерб производительности сети [§6.5 RFC 1347].
Второй подход привлекателен тем, что сразу же дает нам численные оценки, но насколько безупречна логическая связь между числом каких-то частиц и размером нового адресного пространства? Конечно, интуитивно понятно: возможностям человека по назначению адресов IP есть передел, и он вряд ли превышает знакомые нам "астрономические" величины. Однако кажущаяся простота этого подхода может оказаться ширмой, которая заслонит от нас технически обоснованные критерии выбора из области TCP/IP, а не космологии.
Кроме того, нечеткость мысли нередко превращается в привычку и влечет за собой грубые просчеты. Выбирая наугад верхнюю оценку необходимого числа адресов, "природники" порой ленятся подвергнуть критическому анализу даже собственные гипотезы. Яркий пример этого можно найти в одном из ранних проектов "нового IP", чьи авторы рассчитали необходимый размер адресного пространства, исходя из суммарного числа байтов на всех сетевых ресурсах Internet [RFC 1475]. При этом они предполагали, что один ресурс никогда не станет содержать больше 4 гигабайт [§2.1 RFC 1475]. Очевидно, что проблема здесь вовсе не в точности оценки размера сетевого ресурса через 10 лет, а в самой постановке задачи.
И все-таки любопытно, каковы природные сверхвеличины? Оказывается, их порядок был известен еще Архимеду. Демонстрируя возможности науки
перед царем Гелоном, Архимед построил весьма убедительную для своего времени
модель8
Архимед. Исчисление песчинок (псаммит). М.-Л.: Гос. Технико-теоретическое изд-во, 1932. 104 с.
., согласно которой в объеме вселенной умещается
 песчинок. Современные астрофизические теории говорят не о песчинках, а об атомах, которых в модельной вселенной насчитывается, по
разным оценкам, порядка
песчинок. Современные астрофизические теории говорят не о песчинках, а об атомах, которых в модельной вселенной насчитывается, по
разным оценкам, порядка  штук. Если принять средний диаметр песчинки равным 300 мкм, плотность — 2,4 г/см3 (кварц), а средний
вес составляющих ее атомов — ~30 атомных единиц (SiO2), то в одной такой песчинке содержится порядка
штук. Если принять средний диаметр песчинки равным 300 мкм, плотность — 2,4 г/см3 (кварц), а средний
вес составляющих ее атомов — ~30 атомных единиц (SiO2), то в одной такой песчинке содержится порядка 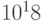 атомов, а в Архимедовой
вселенной их всего
атомов, а в Архимедовой
вселенной их всего 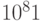 , что не выходит за пределы сегодняшних представлений. Таким образом, оказывается, что сила научного воображения
— величина практически постоянная еще с античных времен.
, что не выходит за пределы сегодняшних представлений. Таким образом, оказывается, что сила научного воображения
— величина практически постоянная еще с античных времен.
А что же заслоняет от нас хромая логика второго подхода? Она неявно примиряет нас с той мыслью, что все адреса IPv6 тоже когда-то будут розданы и все, на что мы способны, это отодвинуть роковой день как можно дальше в будущее. Иначе говоря, этот подход рассматривает адресное пространство как аморфную кучу песчинок, из которой их черпают, неважно, по одной, ведрами или ковшом экскаватора. В действительности же у адресного пространства всегда возникает определенная структура, и нам пора ее сознательно формировать, потому что именно от нее будет напрямую зависеть срок службы адресного пространства IPv6. Взамен мы будем вознаграждены вполне обоснованной оценкой его требуемого размера.
Прежде всего, обратим внимание, что интересующий нас адрес в любом случае будет двоичный (цепочка битов), а распределять двоичные адреса
удобнее всего не по одному или произвольными диапазонами, а в виде префиксов. Мы уже знакомы с этой процедурой в контексте IPv4. Субъект
распределительной иерархии получает сверху определенный двоичный префикс, дополняет его несколькими битами и спускает удлиненный префикс
уровнем ниже. Для простоты допустим, что он дополняет префикс постоянным числом битов n. Тогда данный субъект сможет превратить полученный
сверху префикс в не более чем 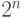 префиксов для субъектов нижележащего уровня. Скажем, получив "сверху" (например, от LIR) префикс IPv4
198.51.100.128/25 и полагая n = 2, можно произвести четыре префикса /27 для раздачи нижестоящим субъектам (например, рядовым пользователям)
: 198.51.100.128/27, 198.51.100.160/27, 198.51.100.192/27, и 198.51.100.224/27.
префиксов для субъектов нижележащего уровня. Скажем, получив "сверху" (например, от LIR) префикс IPv4
198.51.100.128/25 и полагая n = 2, можно произвести четыре префикса /27 для раздачи нижестоящим субъектам (например, рядовым пользователям)
: 198.51.100.128/27, 198.51.100.160/27, 198.51.100.192/27, и 198.51.100.224/27.
Что делать нашему субъекту, когда он исчерпает выданный ему префикс? Видимо, запросить сверху еще один. Затем он тоже исчерпывается, и опять требуется новый префикс, чтобы поддержать рост сети. Через некоторое время каждый субъект обладает набором разрозненных префиксов, которые не агрегируются, потому что получены из разных префиксов вышестоящего уровня. К примеру, 198.51.100.128/25 не агрегируется с 203.0.113.0/25, хотя он мог бы агрегироваться с 198.51.100.0/25, дав один префикс 198.51.100.0/24, — но, увы, к этому моменту 198.51.100.0/25 уже выдан в совсем другие руки. Именно так произошло дробление адресного пространства в IPv4.
Но что плохого в дроблении адресного пространства? Во-первых, это увеличивает административные расходы, так как каждому субъекту приходится учитывать множество полученных и выданных префиксов, хотя в идеале он мог бы получить сверху ровно один префикс и выдать по одному префиксу каждому подчиненному субъекту. Во-вторых, числу неагрегируемых префиксов пропорционально число маршрутов, которые возникнут в сети. К примеру, в "зоне без умолчания" (default free zone), составляющей ядро Internet, число субъектов (автономных систем) на январь 2010 года составило примерно 30 000, а число неагрегируемых маршрутов IPv4 — 150 0009 P. Smith. BGP Routing Table Analysis. APNIC. http://thyme.apnic.net/ , и это различие в пять раз вызвано, в основном, дроблением адресного пространства IPv4.
Чтобы эта проблема не возникла вновь, адресное пространство IPv6 должно быть практически неисчерпаемым на всех уровнях распределительной иерархии: каждому субъекту иерархии должно хватить одного префикса. Обратите внимание: из сказанного не следует, что мы должны запретить назначение субъекту нескольких префиксов. В некоторых случаях это полезный и технически обоснованный прием. Однако плохо, когда хроническая нехватка адресов вынуждает к постоянному и повсеместному его использованию: пользователи выпрашивают дополнительные префиксы у провайдера, тот — у региональной регистратуры и т.д.

 "
"