Функциональные зависимости и реляционные базы данных
Алгоритмы построения минимального покрытия
Алгоритм MINIMAZE (G)
input: Множество ФЗ G
output: Минимальное покрытие G
F = NONREDUN ( G )
Построить непустые множества Еf(X)+, состоящие из ФЗ, с левой частью,
эквивалентной Х. Ef(X) - подмножество Ef(X)+, отвечающее атрибуту Х.
for any Ef(X) из Ef(X)+ do
for any Y -> U из Ef(X) do
for any Z -> V <> Y->U из Еf(X) do
if DDERIVERS ( F, Y, -> Z ) then
заменить Y->U и Z->V на Z->UV в F
Return(F)Примеры. Построение минимального покрытия ФЗ
Пусть F = {AB -> C, C -> A, BC -> D, ACD -> B, D -> EG, BE -> C, CG -> BD, CE -> AG}.
Расщепив правые части с помощью правила декомпозиции, получим
AB -> C, C -> A, BC -> D, ACD -> B, D -> E, D -> G, BE -> C, CG -> B, CG -> D, CE -> A, CE -> G}.
CE -> A - избыточна, так как следует из C -> A.
CG -> B - избыточна, так как следует из CG -> D, C -> A, ACD -> B.
Больше избыточных ФЗ нет.
ACD -> B может быть замещена CD -> В, так как C -> A.
Первое МП:
AB -> C, C -> A, BC -> D, CD -> B, D -> E, D -> G, BE -> C, CG -> D, CE -> G.
Построим второе МП, исключив CE -> A, CG -> D, AC -> DB:
AB -> C, C -> A, BC -> D, D -> E, D -> G, BE -> C, CG ->В, CE -> G
Так же как и для F -зависимостей, можно определить правила вывода для многозначных MV -зависимостей, и определить их взаимоотношения с F -зависимостями, а далее показать совместную полноту правил вывода F - и MV -зависимостей.
Правила вывода для MV-зависимостей:
- Дополнение. Если
 и задана МФЗ
и задана МФЗ  , то имеет место МФЗ
, то имеет место МФЗ 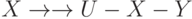 .
. - Пополнение. Если
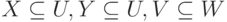 и задана МФЗ X Y, то имеет место МФЗ
и задана МФЗ X Y, то имеет место МФЗ 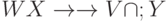 .
. -
Транзитивность. Если
 и заданы МФЗ
и заданы МФЗ  и МФЗ
и МФЗ 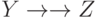 , то имеет место МФЗ
, то имеет место МФЗ 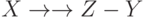 .
. - Объединение. Если
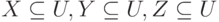 и заданы МФЗ
и заданы МФЗ  и МФЗ
и МФЗ  , то имеет место МФЗ
, то имеет место МФЗ  .
. - Псевдотранзитивность. Если
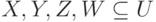 и заданы МФЗ
и заданы МФЗ  и МФЗ
и МФЗ  , то имеет место МФЗ
, то имеет место МФЗ 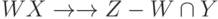 .
. - Смешанная транзитивность. Если
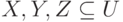 и заданы МФЗ
и заданы МФЗ  и ФЗ
и ФЗ  , то имеет место ФЗ
, то имеет место ФЗ 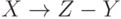 .
. - Декомпозиция. Если
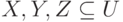 и заданы МФЗ
и заданы МФЗ  и МФЗ
и МФЗ  то имеют место МФЗ
то имеют место МФЗ  , МФЗ
, МФЗ 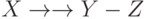 , МФЗ
, МФЗ 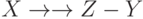 .
.
Совместные правила вывода для F - и MV -зависимостей:
- Если
 и задана ФЗ
и задана ФЗ 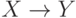 , то имеет место МФЗ
, то имеет место МФЗ  .
. - Если
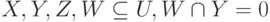 и заданы МФЗ
и заданы МФЗ  и ФЗ
и ФЗ 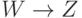 , то имеет место ФЗ
, то имеет место ФЗ 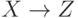 .
.
Справедливо следующее утверждение: система правил вывода F1-F3, MV1-MV3, FMV1 и FMV2 является надежной и полной.
Правила декомпозиции и объединения MV -зависимостей позволяют сформулировать следующее утверждение. Пусть U - множество атрибутов, тогда можно построить разбиение U-X на множества 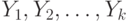 , такое, что при
, такое, что при 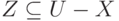 имеет место МФЗ
имеет место МФЗ  , если только Z является объединением некоторого числа Yi. Набор множеств Y1, Y2, ..., Yk называется базисом Х F - и MV -зависимостей. Каждое Yi может состоять из одного атрибута.
, если только Z является объединением некоторого числа Yi. Набор множеств Y1, Y2, ..., Yk называется базисом Х F - и MV -зависимостей. Каждое Yi может состоять из одного атрибута.
Пусть D - множество F - и MV -зависимостей, тогда, так же как и для F-зависимостей, замыкание D+ множества D может быть логически выведено по аксиомам F1-F3, MV1-MV3, FMV1 и FMV2. Однако этот процесс может потребовать времени, пропорционального eL, где L - число ФЗ в D.
На практике часто требуется только знать, следует ли из D конкретная ФЗ  или
или 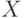 . Этого достаточно, чтобы исключить избыточные ФЗ. Для того чтобы определить, имеет ли место MV -зависимость
. Этого достаточно, чтобы исключить избыточные ФЗ. Для того чтобы определить, имеет ли место MV -зависимость  , достаточно построить базис Х зависимостей и посмотреть, является ли Z - X объединением каких-либо его множеств. Для вычисления базиса зависимостей Х относительно D достаточно найти базис относительно множества МФЗ М, где М состоит из а) всех МФЗ из D и б) множества МФЗ
, достаточно построить базис Х зависимостей и посмотреть, является ли Z - X объединением каких-либо его множеств. Для вычисления базиса зависимостей Х относительно D достаточно найти базис относительно множества МФЗ М, где М состоит из а) всех МФЗ из D и б) множества МФЗ  для каждой ФЗ
для каждой ФЗ 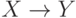 в D, где
в D, где 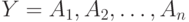 .
.
Ниже приведен алгоритм вычисления базиса Х ФЗ относительно M.
Алгоритм вычисления базиса функциональных зависимостей
input: Множество MV-зависимостей М на множестве атрибутов
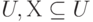
output: Базис Х относительно М.
- Пусть Т - множество множеств
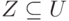 , таких, что для некоторой МФЗ
, таких, что для некоторой МФЗ 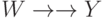 в M имеем
в M имеем 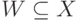 , и Z есть либо Y - X, либо U - X - Y.
, и Z есть либо Y - X, либо U - X - Y. - До тех пор, пока Т не превратится в совокупность непересекающихся множеств, будем искать в нем очередную пару пересекающихся множеств Z1, Z2 и заменять ее множествами
 , отбрасывая пустое множество
, отбрасывая пустое множество 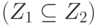 . В результате получим множество S.
. В результате получим множество S. - До тех пор, пока возможны изменения во множестве S, будем искать МФЗ
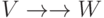 в М и некоторое множество Y в S, такие, что Y пересекается с W, но не пересекается с V. Заменяем Y в S на
в М и некоторое множество Y в S, такие, что Y пересекается с W, но не пересекается с V. Заменяем Y в S на  и Y - W.
и Y - W. - Полученная совокупность множеств S есть базис Х ФЗ.
Теория функциональных зависимостей на отношениях реляционной базы данных представляет собой математический фундамент, на котором строится проектирование реляционных баз данных. Подытожим сведения о функциональных зависимостях, полученных в данном учебном элементе.
- Аксиомы вывода ФЗ позволяют производить формальное (алгебраическое) манипулирование зависимостями разных классов: F- и MV -зависимостями. В рамках данных аксиом преобразования схем отношений реляционных баз данных будут эквивалентными.
- Аксиомы вывода ФЗ позволяют оперировать отдельными атрибутами зависимостей, при этом сами ФЗ сохраняются: атрибуты из правой части ФЗ могут быть удалены; атрибуты из левой части ФЗ могут быть удалены, если удаляемый атрибут отсутствует в правой части; независимо от того, перекрываются ли множества атрибутов или нет, любые атрибуты из исходного множества можно одновременно подставлять в правую и левую части ФЗ. Несущественные зависимости могут быть удалены, а затем восстановлены.
- Существует минимальный набор ФЗ, который позволяет восстановить исходный набор ФЗ. Это обстоятельство позволяет теоретически обосновать и практически проводить эквивалентные, сохраняющие семантический смысл данных, преобразования схем отношений реляционной базы данных.
Литература: [3], [11], [14], [15], [20], [31], [43], [44], [45].
