|
Здравствуйте,ясдавала 15 тестов и экзамен. Мне нужно сейчас посмотреть результаты тестов.Как это сдлеать? |
Введение в моделирование объектов, процессов и явлений
Модель и моделирование – это универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания объекта, процесса, явления (через модели и моделирование ).
Модели и моделирование объединяют специалистов различных областей, работающих над решением межпредметных проблем, независимо от того, где эта модель и результаты моделирования будут применены.
Модель – это некоторое представление или описание оригинала (объекта, процесса, явления), которое при определенных предложениях, гипотезах о поведении оригинала позволяет замещать оригинал для его лучшего изучения, исследования, описания его свойств.
Пример. Рассматривая физическое тело, брошенное с высоты h и падающее свободно в течение t времени, можно записать соотношение: h = gt2/2 . Это физико-математическая модель системы (математическая модель физической системы) пути при свободном падении тела. При построении этой модели приняты следующие гипотезы: 1) падение происходит в вакууме (то есть коэффициент сопротивления воздуха равен нулю); 2) ветра нет; 3) масса тела неизменна; 4) тело движется с одинаковым постоянным ускорением g в любой точке.
Слово "модель" (лат. modelium) означает "мера", "способ", "сходство с какой-то вещью".
Проблема моделирования состоит из трех взаимосвязанных задач: построение новой (адаптация известной) модели ; исследование модели (разработка метода исследования или адаптация, применение известного); использование (на практике или теоретически) модели.
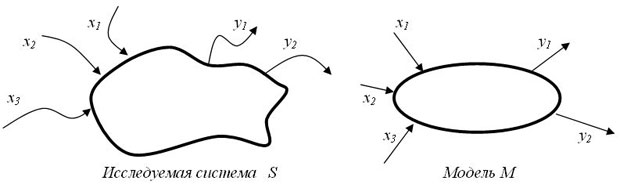
Схема построения модели М системы S с входными сигналами X и выходными сигналами Y изображена на рис. 13.1.
Если на вход М поступают сигналы из X и на выходе появляются сигналы из Y, то задан закон, правило f функционирования модели, системы.
Классификацию моделей проводят по различным критериям.
Модель – статическая, если среди параметров описания модели нет (явно) временного параметра.
Модель – динамическая, если среди параметров модели явно выделен временной параметр.
Модель – дискретная, если описывает поведение оригинала лишь дискретно, например в дискретные моменты времени (для динамической модели ).
Модель – непрерывная, если описывает поведение оригинала на всем промежутке времени.
Модель – детерминированная, если для каждой допустимой совокупности входных параметров она позволяет определять однозначно набор выходных параметров; в противном случае – модель недетерминированная, стохастическая (вероятностная) .
Модель – функциональная, если представима системой функциональных соотношений (например, уравнений).
Модель – теоретико-множественная, если представима некоторыми множествами и отношениями их и их элементов.
Модель – логическая, если представима предикатами, логическими функциями и отношениями.
Модель – информационно-логическая, если она представима информацией о составных элементах, подмоделях, а также логическими отношениями между ними.
Модель – игровая, если она описывает, реализует некоторую игровую ситуацию между элементами (объектами и субъектами игры).
Модель – алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование, развитие. Введение такого, на первый взгляд, непривычного типа моделей (действительно, кажется, что любая модель может быть представлена алгоритмом ее исследования), на наш взгляд, вполне обосновано, так как не все модели могут быть исследованы или реализованы алгоритмически.
Модель – графовая, если она представима графом (отношениями вершин и соединяющих их ребер) или графами и отношениями между ними.
Модель – иерархическая (древовидная), если она представима иерахической структурой (деревом).
Модель – языковая, лингвистическая, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой. Иногда такие модели называют вербальными, синтаксическими и т.п.
Модель – визуальная, если она позволяет визуализировать отношения и связи моделируемой системы, особенно в динамике.
Модель – натурная, если она есть материальная копия оригинала.
Модель – геометрическая, если она представима геометрическими образами и отношениями между ними.
Модель – имитационная, если она построена для испытания или изучения, проигрывания возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.
Есть и другие типы моделей.
Пример. Модель F = am – статическая модель движения тела по наклонной плоскости. Динамическая модель типа закона Ньютона: F(t) = a(t)m(t) или, еще более точно и лучше, F(t)=s''(t)m(t). Если рассматривать только t = 0.1, 0.2, …, 1 (с), то модель St = gt2/2 или числовая последовательность S0 = 0, S1 = 0.01g/2, S2 = 0.04g, …, S10 = g/2 может служить дискретной моделью движения свободно падающего тела. Модель S = gt2/2, 0 < t < 10 непрерывна на промежутке времени (0;10).
Пусть модель экономической системы производства товаров двух видов 1 и 2, соответственно, в количестве x1 и x2 единиц и стоимостью каждой единицы товара a1 и a2 на предприятии описана в виде соотношения a1x1 + a2x2 = S , где S – общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, определяя общую стоимость S в зависимости от тех или иных значений объемов производимых товаров. Приведенные выше физические модели – детерминированные.
Если в модели S= gt2/2, 0 < t < 10 мы учтем случайный параметр – порыв ветра с силой p при падении тела, например, просто так: S(p) = g(p)t2/2, 0 < t < 10 , то мы получим стохастическую модель (уже не свободного!) падения. Это – также функциональная модель.
Для множества X = {Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна} опишем отношения Y: "Николай – супруг Елены", "Екатерина – супруга Петра", "Татьяна – дочь Николая и Елены", "Михаил – сын Петра и Екатерины". Тогда множества X и Y могут служить теоретико-множественной моделью двух семей.