|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы теории игр и исследование операций
Принятие решения и целеполагающая деятельность человека в гуманитарной, социальноэкономической, политико-идеологической, военно-технической сферах тесно связаны. Здесь зачастую недопустимы ошибки, так как они могут привести к пагубным последствиям. Из-за ограниченных возможностей человека и возможных ошибок и возникает необходимость применения научного подхода к обоснованию и принятию решений.
Принятие решений, наряду с прогнозированием, планированием, ситуационным анализом обстановки, исполнением решений, контролем и учетом, является функцией управления. Все функции управления направлены так или иначе на формирование или реализацию решений и любую функцию управления, технологически их можно представить в виде последовательности каких-либо связанных общей целью решений.
Конечным результатом любой задачи принятия решений является решение.
Принятие решения - это выбор одного варианта из некоторого множества рассматриваемых допустимых вариантов. Обычно их число конечно, а каждый вариант выбора определяет некоторый результат (экономический эффект, прибыль, выигрыш, полезность, надёжность и т.д.), допускающий количественную оценку. Такой результат обычно называется полезностью решения. Иначе говоря, отыскивается вариант с наибольшим значением результата. Возможен и подход с минимизацией противоположной оценки, например, отрицательной величины полезности. Часто на практике встречается ситуация, когда каждому варианту решения соответствует единственный результат, хотя возможны и другие случаи, например, когда каждому варианту i и условию j, характеризующему полезность, соответствует результат решения xij. Таким образом, можно говорить о матрице решений |xij|, i=1,2,..., m ; j=1,2,..., m. Чтобы оценить решение, необходимо уметь оценивать все его последствия. Существуют различные подходы для такой оценки. Например, если решения альтернативные, то можно последствия каждого из них характеризовать суммой его наибольшего и наименьшего результатов, максимумом из возможных таких сумм, максимумом из максимумов по всем вариантам (оптимистическая позиция выбора), максимумом из среднего арифметического (нейтральная позиция выбора), максимумом из минимума (пессимистическая позиция) и другими критериями.
Классические модели принятия решений, как правило, являются оптимизационными, ставящими цель: максимизировать выгоду и на основе этих моделей получить практическую прибыль. Так как теоретиков меньше интересует вторая сторона, а практиков - первая, то при разработке и использовании таких моделей необходимо их тесное сотрудничество. Практические рекомендации (решения) могут быть получены, если при построении модели принятия решений придать большее значение учету существенных структурных элементов моделируемой системы, т.е. разработке имитационной модели принятия решений, с привлечением экспериментальных, полуэкспериментальных и теоретических методов. Кроме классических (оптимизационных) процедур принятия решений существуют и ряд базовых неклассических (неоклассических) процедур и технологий, некоторые из которых мы рассмотрим ниже.
Классификация задач принятия решений проводится по различным признакам, среди которых наиболее существенными являются: степень определенности информации; использование эксперимента для получения информации; количество лиц, принимающих решения; содержание решений; направленность решений.
На процесс принятия решения часто воздействуют различные случайные (стохастические) параметры, усложняющие процедуру. Недостаток информации об их распределении (сложность их измерения) приводят к необходимости принятия каких-то гипотез как об области их изменения, так и о характере распределения (о функции распределения вероятностей). Правильность используемых гипотез необходимость проверять с помощью методов оценки статистических гипотез. При отсутствии достаточной информации для такой процедуры приходиться привлекать большое число типов распределения. Проблемы принятия решений с недетерминированными параметрами называют проблемами принятия решений в условиях недостатка информации . Чем меньше у нас информации, тем больше может оказаться различие между ожидаемым и действительным результатами принимаемых решений в целом. Мера влияния информации (параметров) на результат решения называется релевантностью. Особо важно в социально-экономической сфере принятие решения при наличии риска (неплатежей, невозврата кредитов, ухудшения условий жизни и т.д.).
Формализуемые решения принимаются на основе соответствующих математических методов (алгоритмов). Математическая модель задачи оптимизации формализуемого решения включает следующие элементы:
- задаваемую оптимизируемую целевую функцию (критерий управляемости):
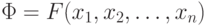 , где xi, i=1,2,...,n - параметры, учитываемые при принятии решения (отражающие ресурсы принятия решений);
, где xi, i=1,2,...,n - параметры, учитываемые при принятии решения (отражающие ресурсы принятия решений); - условия, отражающие ограниченность ресурсов и действий лица принимающего решение (ЛПР): g_i(x_j)<a_i, ki(xj)=bi ; cj<xj<di, i=1,2,...,m ; j=1,2,..., n.
Непременное требование для решения задачи оптимизации - n>m.
В зависимости от критерия эффективности, стратегий и факторов управления выбирается тот или иной метод (алгоритм) оптимизации.
Общая процедура принятия решений может состоять из следующих этапов:
- анализ проблемы и среды (цели принятия решения, их приоритеты, глубина и ограничения рассмотрения, элементы, связи, ресурсы среды, критерии оценки);
- постановка задачи (определение спецификаций задачи, альтернатив и критериев выбора решения);
- выбор ( адаптация, разработка ) метода решения задачи ;
- выбор ( адаптация, разработка ) метода оценки решения ;
- решение задачи (математическая и компьютерная обработка данных, имитационные и экспертные оценки, уточнение и модификация, если это необходимо);
- анализ и интерпретация результатов.
Выбор решения - заключительный и наиболее ответственный этап процесса. В реальных задачах принятия решений, к началу этапа выбора еще сохраняется большая неопределенность, поэтому сразу осуществить выбор единственного решения из множества допустимых практически очень сложно. Поэтому используется принцип последовательного уменьшения неопределенности, который заключается в последовательном трёхэтапном (обычно) сужении множества решений. На первом этапе исходное множество альтернативных решений Y сужается (используя ограничения на ресурсы) до множества приемлемых или допустимых решений  . На втором этапе множество допустимых решений Y1 сужается (учитывая критерий оптимальности) до множества эффективных решений
. На втором этапе множество допустимых решений Y1 сужается (учитывая критерий оптимальности) до множества эффективных решений  . На третьем этапе осуществляется выбор (на основе критерия выбора и дополнительной информации, в том числе и экспертной) единственного решения
. На третьем этапе осуществляется выбор (на основе критерия выбора и дополнительной информации, в том числе и экспертной) единственного решения 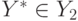 .
.
Система принятия решений - организованная совокупность ЛПР, методического, программно-технического, информационно-логического и технологического обеспечения принятия решений для достижения целей.
При выборе pационального pешения необходимо принимать во внимание внешнюю сpеду и побочные явления, динамическую изменчивость критериев оценок решения, необходимость ранжирования аспектов и приоритетов решения, их неполноту и разнородность (а иногда и конфликтность, антагонизм).
