|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы дискретного математического анализа
Рассмотрим следующую задачу - численное дифференцирование или численное вычисление производной. Можно вычислить производную любой функции, если она задана аналитически. Для функции, заданной сложным образом или таблично, используют какую-либо интерполяционную функцию. После ее нахождения, дифференцируют найденную функцию (интерполяционная функция представляет собой, как правило, многочлен, поэтому ее дифференцирование не вызывает трудностей).
Решим теперь задачу нахождения наибольшего (наименьшего) значения функции f(x) на заданном отрезке [a;b]. Это задача одномерной оптимизации. Один из простых и эффективных методов поиска минимума такой функции - метод золотого сечения. Он состоит в построении последовательности отрезков [ai;bi] ; i=0, 1, 2,..., стягивающихся к одной точке минимума функции f(x). Вначале выбираются две точки  ,
,  из [a0;b0] и вычисляются f(x1), f(x2). Минимум достигается в одном из отрезков, прилегающих к x1 (считаем для определенности f(x1)<f(x2) ), поэтому отбрасываем [x2;b0]. На втором шаге выбираем a1=a ; b1=x2 и т.д. Процесс продолжается до тех пор, пока длина очередного отрезка [an;bn] не станет меньше заданного малого числа e - точности нахождения минимума. Точки xi размещаются на отрезке [ai;bi] так, чтобы выполнялось правило золотого сечения:
из [a0;b0] и вычисляются f(x1), f(x2). Минимум достигается в одном из отрезков, прилегающих к x1 (считаем для определенности f(x1)<f(x2) ), поэтому отбрасываем [x2;b0]. На втором шаге выбираем a1=a ; b1=x2 и т.д. Процесс продолжается до тех пор, пока длина очередного отрезка [an;bn] не станет меньше заданного малого числа e - точности нахождения минимума. Точки xi размещаются на отрезке [ai;bi] так, чтобы выполнялось правило золотого сечения: 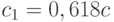 ;
;  , где c - длина оставляемого интервала [ai;bi].
, где c - длина оставляемого интервала [ai;bi].
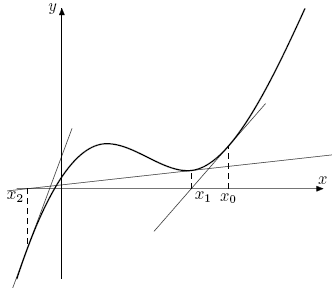
Если оптимизируемая функция - дважды непрерывно дифференцируема, то отыскание минимума функции f(x) производится с помощью стационарной точки, то есть точки x* удовлетворяющей уравнению f'(x*)=0 при помощи метода Ньютона. Если xk - точка, полученная на k -ом этапе, то функция f'(x) аппроксимируется своим уравнением касательной z=f'(xk)+(x-xk) f''(xk), а точка xk+1 выбирается как пересечение этой прямой с осью Ox (рис. 13.1):
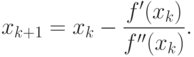
Пример. Вычислительные эксперименты методом Ньютона для функции f(x)=sin x+0,25 на отрезке [0; 3,14] при e=0,0005. Строим таблицу:
| N | k | x0 | x* | xk | f(x*) |
|---|---|---|---|---|---|
| 1 | 12 | 0 | 1,2501 | 1,2509 | 1,5707 |
| 2 | 9 | 0,1 | 1,2500 | 1,2508 | 1,5706 |
| 3 | 8 | 0,4 | 1,2501 | 1,2509 | 1,5708 |
| 4 | 6 | 1 | 1,2500 | 1,2507 | 1,5707 |
Рассмотрим задачу численного решения обыкновенного дифференциального уравнения, а именно, задачи Коши для уравнения первого порядка: y'(x)=f(x,y), y(x0)=y0 на отрезке [a;b] . Идея всех приближенных методов решения этой задачи состоит в том, что отрезок [a;b] разбивается на части точками xi, i=0, 1, ..., n, x0=a, xn=b и производная на каждом из таких отрезков заменяется (аппроксимируется) его дискретным приближением с какой-то точностью. Наиболее простая схема аппроксимации уравнения - схема Эйлера: 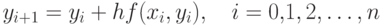 .
.
Пример. Решить задачу Коши: y'=2(x2+y), y(0)=1, 0<x<1. Разобьем отрезок [0;1] на 10 равных частей, то есть h=0,1. Вычисления по схеме Эйлера дают приближенное решение (приведено в таблице).
| i | xi | Приближенное решение | Точное решение |
|---|---|---|---|
| 0 | 0,00 | 1,00 | 1,00 |
| 1 | 0,10 | 1,20 | 1,22 |
| 2 | 0,20 | 1,44 | 1,50 |
| 3 | 0,30 | 1,74 | 1,84 |
| 4 | 0,40 | 2,10 | 2,28 |
| 5 | 0,50 | 2,56 | 2,83 |
| 6 | 0,60 | 3,12 | 3,52 |
| 7 | 0,70 | 3,81 | 4,39 |
| 8 | 0,80 | 4,67 | 5,49 |
| 9 | 0,90 | 5,74 | 6,86 |
| 10 | 0,10 | 7,05 | 8,58 |
Выпуклым множеством называется множество, которое содержит для каждых двух своих точек также и отрезок, соединяющий эти точки.
Теорема. Множеством решений системы m линейных неравенств с n переменными является выпуклый многогранник в n -мерном пространстве.
Пример. Построим множество решений системы линейных неравенств:

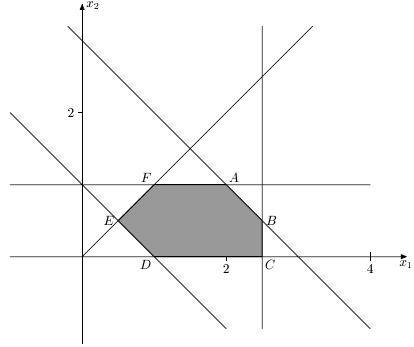
Построим прямые x1+x2=3 ; x1+x2=1 ; x1=x2 ; x1=2,5 ; x2=0 ; x2=1. Заштрихованная область (рис. 13.2) соответствует искомому многоугольнику.
Точки A, B, C, D, E, F - угловые точки множества. Такие точки примечательны и тем, что если отыскивается наибольшее или наименьшее значение линейной функции при указанных ограничениях, условиях типа неравенств (в этом выпуклом множестве), то это значение достигается только в угловых точках. Например, если мы ищем минимум значений функции y=3x1+4x2 при указанных выше ограничениях, то его нужно выбирать из значений y(A)=y(2;1)=6+4=10 ; y(B)=y(2;5)=26 ; y(C)=y(2,5;0)=7,5 ; y(D)=y(1;0)=3 ; y(E)=y(0,5;0,5)=3,5 ; y(F)=y(1;1)=7. Следовательно, наименьшее значение функции при заданных выше ограничениях будет равно 3, и она принимает это значение в точке D. Наибольшее значение y=26 будет достигаться в точке B. Координаты всех точек были найдены совместным решением уравнений двух прямых, пересекающихся в этой точке, например, для нахождения координат точки E решалась система:
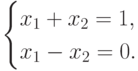
Методы нахождения каких-то оптимальных решений (при каких-то ограничениях, ресурсах) составляют целую область математики, называемую математическим программированием. Она изучает методы, алгоритмы решения задач оптимального планирования, управления, прогнозирования.
Основные методы математического программирования - методы нахождения оптимума функции одной или нескольких переменных с ограничениями на область, где отыскивается этот оптимум (максимум или минимум), или без таких ограничений. При этом функция, оптимум которой отыскивается (она называется целевой функцией, функцией цели), может быть линейной или нелинейной, ограничения на область допустимых решений могут быть линейного или нелинейного типа, принимаемые функцией цели значения - целочисленного или нецелочисленного типа, цели - однокритериальные и многокритериальные, целевая функция - аналитической (формулой) или табличной и т.д.
Пример(Транспортная модель).
Пусть некоторая продукция, например, сталь, производится на заводах  . Пусть ai - ежегодный выпуск стали на i -ом заводе
. Пусть ai - ежегодный выпуск стали на i -ом заводе 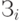 . Пусть эта сталь требуется на рынках Pj, j=1, 2, ..., n. Ежегодная потребность j -ого рынка в стали равна bj. Пусть cij - стоимость перевозки единицы товара с завода
. Пусть эта сталь требуется на рынках Pj, j=1, 2, ..., n. Ежегодная потребность j -ого рынка в стали равна bj. Пусть cij - стоимость перевозки единицы товара с завода 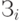 на рынок Pj, а рынки и заводы соединены некоторыми путями. Задача состоит в определении такого плана перевозок, при котором:
на рынок Pj, а рынки и заводы соединены некоторыми путями. Задача состоит в определении такого плана перевозок, при котором:
- удовлетворяется спрос bj на каждом рынке Pj ;
- не превышается предложение ai каждого завода
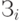 ;
; - минимальна полная цена S всех перевозок.
План перевозок состоит из mn неотрицательных чисел xij, где xij - количество продукции, которое должно перевозиться от
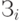 на Pj. Тогда сумма - полное количество продукции, привозимой на рынок Pj.
Условие 1) записывается в виде:Полное количество продукции, вывозимое из завода
на Pj. Тогда сумма - полное количество продукции, привозимой на рынок Pj.
Условие 1) записывается в виде:Полное количество продукции, вывозимое из завода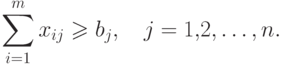
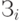 на все рынки Pj, равно сумме всех xij по всем рынкам и по всем заводам (по всем i=1,2,..., m ; j=1,2,...,n ) и, таким образом,
условие 2) эквивалентно соотношениюЦена всех перевозок между всеми
на все рынки Pj, равно сумме всех xij по всем рынкам и по всем заводам (по всем i=1,2,..., m ; j=1,2,...,n ) и, таким образом,
условие 2) эквивалентно соотношениюЦена всех перевозок между всеми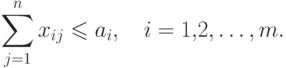
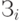 и Pi равнаи, следовательно, условие 3) можно записать в виде:
и Pi равнаи, следовательно, условие 3) можно записать в виде: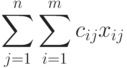
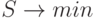 .
.
При этом должны быть выполнены естественные условия:
- неотрицательности перевозимой продукции:
 ;
; - предложение не должно быть меньше спроса:
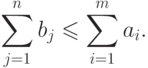
Следовательно, данная экономическая (транспортная) задача сведена к математической задаче: минимизировать линейную целевую функцию S при линейных ограничениях, выраженных вышеприведенными неравенствами. Минимум функции S является конечной целью оптимального планирования (получения минимальной стоимости перевозок). Эта функция называется целевой функцией транспортной задачи, она описывает (скалярно) степень достижения цели.
Для решения линейных задач математического программирования (линейные ограничения, линейная целевая функция) используется один из известных методов - симплексный метод.