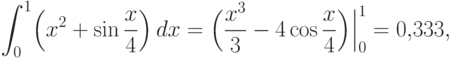|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Элементы дискретного математического анализа
Геометрически интерполяция состоит в нахождении по точкам Mi(xi;yi), i=1, 2,..., n на графике y=f(x), некоторой плавной кривой y=F(x), проходящей через эти точки и мало отклоняющейся от графика y=f(x) в других точках.
Таких функций может быть много - задача интерполяции не имеет единственного решения. Обычно стараются выбрать наиболее простую по форме и наиболее точную интерполянту, например, многочлен вида F(x)=anxn+an-1xn-1+an-2xn-2+...+a0. Покажем на примере, как находить интерполянту.
Пример. Пусть дана дискретная функция
Подберем для этой функции интерполянту - многочлен 2-го порядка: F(x)=ax2+bx+c. Подставив значения в трех точках x=0, x=1, x=2 поочередно в функцию F(x), получаем систему из уравнений вида: F(0)=c=1, F(1)=a+b+c=-2, F(2)=4a+2b+c=3. Решая, мы найдем неизвестные коэффициенты интерполянты: a=4, b=-7, c=1, то есть найдем интерполянту F(x)=4x2-7x+1.Рассмотрим задачу аппроксимации: задана табличная функция
Найти функцию z=f(x), легко вычисляемую и легко записываемую, которая приближенно заменяет (аппроксимирует) данную табличную функцию, причем в отличие от задачи интерполяции мы уже не требуем тут непосредственного совпадения с заданной табличной функцией в заданных точках. Достаточно лишь малого отклонения от них в этих точках, как и в любых других точках области задания функции.Найденная при этом функция y=f(x) называется эмпирической функцией (или формулой), или аппроксимирующей функцией, математической моделью.
Мы рассмотрим нахождение эмпирической функции в виде многочлена Pn(x) = anxn + an-1xn-1 + ... + a1x+a0.
Исследуемая величина y может зависеть также и от нескольких независимых факторов - x1, x2,..., xn: y=y(x1, x2,..., xn). Будем предполагать, что между x и y есть однозначное соответствие, которое и будем искать.
Пусть формула содержит неизвестные параметры функциональной зависимости, т.е. y=f(x, a0, a1,..., am). Конкретные числовые значения этих параметров, соответствующие данному набору y1, y2,..., yn, выбирают из условия наилучшего, в каком-то смысле, согласования теоретических y(xi) и экспериментальных yi данных (i=1, 2,..., n). Наиболее широко применяемый критерий близости - критерий метода наименьших квадратов. Рассмотрим его на примере наиболее часто выбираемой в качестве эмпирической функции - многочлена y=Pm(x)=a0+a1x+...+ amxm. Необходимо найти неизвестные параметры ai, i=1, 2,...,n. Если бы измерения были точны, то для определения m+1 неизвестных a0, a1,..., am достаточно было бы сделать m+1 измерение - в точках x1, x2,..., xm+1, затем подставить в формулу и получить систему m+1 линейных алгебраических уравнений вида:  ,
которую можно решить, например, методом Гаусса. На практике же значения
,
которую можно решить, например, методом Гаусса. На практике же значения  , i=1,...,n искажены (допускаемыми приборами и методикой измерения), то есть на самом деле
, i=1,...,n искажены (допускаемыми приборами и методикой измерения), то есть на самом деле 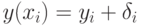 , i=1,2,..., n, где
, i=1,2,..., n, где  - ошибки измерений. Из этих равенств получаем
- ошибки измерений. Из этих равенств получаем

 . Величины
. Величины  называются невязками . Числа a0, a1,..., am определяют из условия минимума суммы квадратов невязок:
называются невязками . Числа a0, a1,..., am определяют из условия минимума суммы квадратов невязок: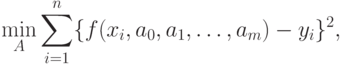
Сумму можно рассматривать как функцию от m+1 параметра (параметров):
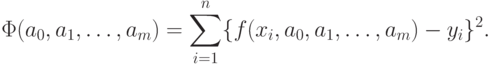
Из условия минимума этой суммы получаем систему так называемых нормальных уравнений (или нормальную систему уравнений):
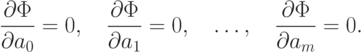
В случае полинома получаем функционал вида
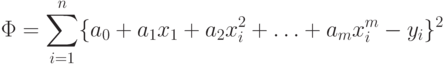
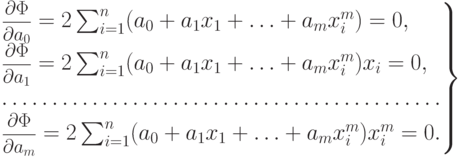
Пример. Рассмотрим функцию, заданную нижеследующей таблицей.
Будем искать линейную зависимость y=a0x+a1. Этот вид зависимости мы выбрали только по критерию наибольшей простоты, хотя по изменениям значений функции видно, что такая зависимость хорошо "работает" только при x=1,5 ; 1,7 ; 1,8 и совсем "плоха" для последних двух значений. Находим нормальную систему: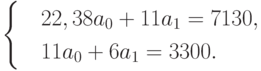
Рассмотрим теперь новый класс задач - численное вычисление определенных интегралов или численное интегрирование.
Пусть f(x) - непрерывная (а поэтому и интегрируемая) на отрезке [a;b] функция. Если F(x) есть первообразная для f(x) на интервале, содержащем отрезок [a;b], то задача интегрирования через элементарные функции для большинства функций разрешима. Если первообразная функция не выражается через элементарные функции ("интеграл не берется в квадратурах"), то нужно использовать численное интегрирование.
Задача численного интегрирования состоит в нахождении интеграла на отрезке [a;b] заменой подынтегральной функции f(x) на этом отрезке [a;b] другой, интерполирующей или аппроксимирующей функцией g(x) (например, многочленом).
Пусть функция f(x) считается заданной в n+1 равноотстоящих точках: a=x0, x1, x2,..., xn-1, xn=b. Соответствующие значения равны: f(xi)=yi, i=0,1, 2,... n, h=xi-xi-1. Формула носит название формулы трапеции, так как при f(x)>0 приближенное значение интеграла слева получается в виде суммы площадей n трапеций:
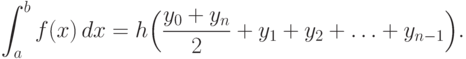
Пример. Вычислить интеграл от 0 до 1 от функции вида y=x2+sin (x/4). Используем точки xi=0,i, i=0, 1,..., 10. Найдем значения функции (таблица).
| i | xi | xi/4 | x2+sin(xi/4) |
|---|---|---|---|
| 0 | 0,00 | 0,000 | 0,00000 |
| 1 | 0,10 | 0,025 | 0,01044 |
| 2 | 0,20 | 0,050 | 0,04873 |
| 3 | 0,30 | 0,075 | 0,09131 |
| 4 | 0,40 | 0,100 | 0,16175 |
| 5 | 0,50 | 0,125 | 0,26218 |
| 6 | 0,60 | 0,150 | 0,36262 |
| 7 | 0,70 | 0,175 | 0,49305 |
| 8 | 0,80 | 0,200 | 0,64349 |
| 9 | 0,90 | 0,225 | 0.81393 |
| 10 | 1,00 | 0,250 | 1.00436 |

Так как точное значение интеграла также можно вычислить приближенно: