НОУ ИНТУИТ | Введение в математику. Лекция 7: Предельный переход и непрерывность

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Кабардино-Балкарский государственный университет

Опубликован: 18.04.2007 | Доступ: свободный | Студентов: 12044 / 2526 | Оценка: 4.16 / 4.04 | Длительность: 14:52:00

ISBN: 978-5-9556-0105-2

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Для вычисления таких пределов необходимо преобразовать (раскрыть) неопределенность $\frac {f(x)}{g(x)}$ так, чтобы ее предел уже не давал неопределенность.

Пример.Раскроем некоторые неопределенности:

1.

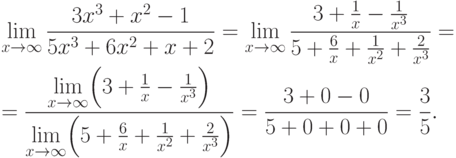
$\displaystyle \lim\limits_{x\to \infty} \frac {3x^3+x^2-1}{5x^3+6x^2+x+2} = \lim\limits_{x\to \infty} \frac {3+\frac 1x-\frac {1}{x^3}} {5+\frac 6x+\frac {1}{x^2}+\frac {2}{x^3} } =\\ \newline= \frac {\lim\limits_{x\to \infty} \Bigl(3+\frac 1x-\frac {1}{x^3} \Bigr)} {\lim\limits_{x\to \infty} \Bigl(5+\frac 6x+ \frac {1}{x^2}+\frac {2}{x^3} \Bigr)} = \frac {3+0-0}{5+0+0+0} =\frac 35.$

2.

$\displaystyle \lim\limits_{x\to 3} \frac {x^2-4x+3}{x^2-9} = \lim\limits_{x\to 3} \frac {x-1}{x+3} =\frac 26=\frac 13.$

3.

$\displaystyle \lim\limits_{x\to 1} \frac {x-1}{\sqrt{x+3}-2} = \lim\limits_{x\to 1} \frac {(x-1)(\sqrt{x+3}+2)} {(\sqrt{x+3}-2)(\sqrt{x+3}+2)} =\\ \newline= \lim\limits_{x\to 1} \frac {(x-1)(\sqrt{x+3}+2)}{x-1} = \lim\limits_{x\to 1} (\sqrt{x+3}+2) =4.$

Теорема.Если 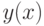y(x) - бесконечно малая величина при 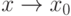$x\to x_0$ , то справедливы следующие соотношения эквивалентности:

$\sin y\sim y, \\ \tg y \sim y, \\ \arcsin y \sim y, \\ \arctg y \sim y, \\ 1-\cos y \sim y^2/2, \\ \log_a(1+y) \sim y, \\ a^y-1\sim y \ln a, \\ (1+y)^n -1 \sim ny, \\ \sqrt[n]{1+y}-1 \sim y/n.$

Пример. В частности, используя 7-е и 9-е соотношения, вычислим

$\displaystyle \lim\limits_{x\to 0} \frac {e^x-1}{\sqrt[3]{1-x}-1} = \lim\limits_{x\to 0} \frac {x}{\frac {1}{3}\cdot (-x)} =-3;$
$\displaystyle \lim\limits_{x\to 0} \frac {\arctg \sqrt{x}}{\sin\sqrt[3]x} = \lim\limits_{x\to 0} \frac {\sqrt{x}}{\sqrt[3]{x}} = \lim\limits_{x\to 0} \sqrt[6]{x}=0.$

Перейдем к функциям многих переменных, ограничиваясь двумя переменными: z=f(x,y).

Последовательность точек M₁(x₁,y₁), M₂(x₂,y₂), ..., M_n(x_n,y_n), ... сходится к точке M₀(x₀,y₀), если для каждой точки M_n расстояние ее до точки M₀ стремится к нулю при 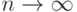$n\to \infty$ : $|\overrightarrow{M_nM_0}| = \sqrt{(x_n-x_0)^2 + (y_n-y_0)^2} \to 0$ .

Пример.Рассмотрим пределы, вычисляемые непосредственной подстановкой координат предельной точки: $\lim\limits_{(x,y)\to (1, 2)}(x^2+y^2-2) =3$ . Наоборот, функция $z=\frac {x^2-y^2}{x^2+y^2}$ при $(x,y)\to (0, 0)$ не имеет предела. Действительно, если выбрать последовательность точек {M_i} = {(x₁,0), (x₂,0), ..., (x_n,0)}, то

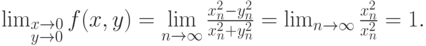
$\lim _{\substack{ {x\to 0} \\ {y\to 0} }} f(x,y) = \lim\limits_{n\to \infty} \frac {x_n^2-y^2_n}{x^2_n+y^2_n} = \lim _{n\to \infty} \frac {x^2_n}{x^2_n} =1.$

Если же выбрать последовательность точек {M_i} = {(0,y₁), (0,y₂), ..., (0,y_n)}, то

$\lim _{\substack{ {x\to 0} \\ {y\to 0} }} f(x,y) = \lim\limits_{n\to \infty} \frac {0-y^2_n}{0+y^2_n} =-1.$

Так как точки M_i выбраны произвольно и предел не должен зависеть от способа выбора точки M_i и способа их стремления к точке M₀(x₀,y₀), то предел функции в этой точке не существует.

Пусть задана функция y=f(x) с областью определения D(f) и областью изменения E(f). Возьмем произвольную точку 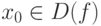$x_0\in D(f)$ и приращение аргумента - число 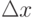$\Delta x$ , такое, что $x=x_0+\Delta x\in D(f)$ . Приращение функции в точке x₀ будет равно (см. рис. 7.3):

$\Delta y=f(x)-f(x_0)=f(x_0+\Delta x)-f(x_0).$

Рис. 7.3. Приращения аргумента и функции

Дадим некоторые определения предела функции (различающиеся своими подходами).

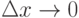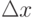Функция y=f(x) называется непрерывной в точке $x_0 \in D(f)$ , если из $\Delta x\to 0$ следует, что $\Delta y\to 0$ , то есть бесконечно малым приращениям $\Delta x$ аргумента x соответствуют бесконечно малые приращения 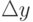$\Delta y$ функции f(x) .

Функция y=f(x) называется непрерывной в точке 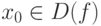$x_0\in D(f)$ , если

Сравнивая это определение с определением предела функции f(x) при 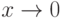$x\to 0$ , заключаем, что можно дать эквивалентное третье определение непрерывной функции.

Функция y=f(x) называется непрерывной в точке 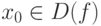$x_0\in D(f)$ , если $\lim _{x\to x_0} f(x) = f(x_0)$ .

Функция, непрерывная в каждой точке $x\in X\subset D(f)$ , называется непрерывной на всем множестве X .

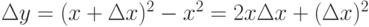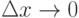Пример.Функция y=x² непрерывна в каждой точке $x_0 \in D(y)$ , поскольку $\Delta y = (x+\Delta x)^2-x^2 =2x\Delta x + (\Delta x)^2$ и если $\Delta x \to 0$ , то $\Delta y \to 0$ .

Если функция y=f(x) в точке x₀ не является непрерывной, то точка x=x₀ называется точкой разрыва функции .

Разрыв у функции может быть по двум причинам:

Точка $x_0\notin D(f)$ и поэтому f(x₀), $f(x_0+\Delta x)$ не определены, или $f(x_0)=\pm \infty$ .
Из того, что 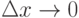$\Delta x\to 0$ , не следует, что $\Delta y\to 0$ .

Пример.Пусть $f(x)=\frac 1x$ . Точка x₀=0 - точка разрыва, так как $f(0)=\infty$ . Функция

$\begin{cases} x, & x\le 0, \\ x+1, & x>0 \end{cases}$

имеет в точке x₀=0 разрыв, так как при $\Delta x>0$ она стремится к 1, а при $\Delta x<0$ - стремится к 0, то есть предел в точке x₀=0 не существует.

Теорема Вейерштрасса.Функция f(x), непрерывная на [a;b], принимает на этом промежутке свое наибольшее (M) и наименьшее (m) значения.

Доказательства (строгого) этой теоремы мы не приводим. Ее суть очевидна геометрически: если график - непрерывная линия на отрезке, на этой линии есть хотя бы одна наиболее "высокая" и наиболее "низкая" точка.

Рассмотрим функцию двух переменных z=f(x,y).

Приращением функции z=f(x,y) по переменной x называется разность вида: $\Delta _xz=f(x+\Delta x,y)-f(x,y)$ , а приращением по y - $\Delta _yz=f(x,y+\Delta y)-f(x,y)$ . Приращение ( полное приращение ) функции - это $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$ .

Непрерывное и дискретное не существуют друг без друга, переходят друг в друга, взаимно дополняют и взаимно обогащают друг друга. Дискретность невозможна без непрерывности при каких-то условиях. Непрерывность реализуется через дискретность.

Пример.Непрерывность функции определяется через дискретность - приращения аргумента и значения функции. Приращения функции невозможно рассматривать ни на одном промежутке $[x;x+\Delta x]$ изменения аргумента, не допустив непрерывности функции на этом промежутке.

Ниже мы рассмотрим и другие примеры непрерывного и дискретного, их взаимодействия и взаимообогащения.

Дальше >>

Авторизоваться

Введение в математику

Предельный переход и непрерывность

Вопросы и ответы