Уравнения и неравенства

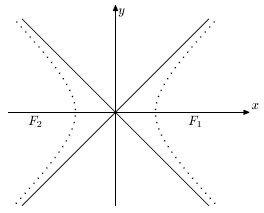
Гипербола - геометрическое место точек (рис. 6.3), разность расстояний от каждой из которых до двух данных точек F₁ и F₂, называемых фокусами, есть величина постоянная. Задается уравнением

Рис. 6.3. График гиперболы

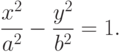
Это уравнение можно вывести, как и вышеприведенное уравнение эллипса.

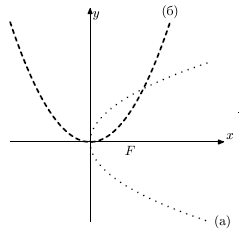
Парабола - геометрическое место точек, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Задается уравнением: y²=2px (рис. 6.4а , директриса параллельна оси Oy ), y=2px² (рис. 6.4б, директриса параллельна оси Ox ).

Рис. 6.4. Графики парабол

Это уравнение можно вывести, как и вышеприведенное уравнение эллипса. Общее неявное уравнение для линий на плоскости имеет вид Ax²+2Bxy+Cy²+Dx+Ey+F=0, где параметры уравнения A, B, C, D, E, F - const.

Уравнение линии задано явно в виде y=f(x), где x, y - координаты точки на плоскости xOy. Если x, а, следовательно, и y, изменяются в зависимости от некоторого параметра t (например, времени), то получим параметрические уравнения линии: x=x(t), y=y(t).

Пример. Если взять за t - угол , то, используя полярные координаты, получим параметрические уравнения окружности:

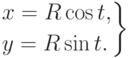
Перейдем от параметрических уравнений к уравнению в прямоугольной системе координат. Для этого, учитывая основное тригонометрическое равенство и координаты x, y текущей точки, получаем: x²+y²=R²(sin²t+cos²t)=1.

Перейдем от параметрических уравнений окружности к уравнению в полярной системе координат; для этого полагаем .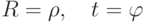

Уравнением линии или поверхности как геометрического места точек в пространстве называется уравнение, которое связывает декартовы координаты x,y,z любой точки, принадлежащей этой линии или поверхности; уравнению линии (поверхности) не удовлетворяют координаты точек, не принадлежащих линии (поверхности).

Итак, уравнение линии (поверхности) будет иметь общий вид: F(x,y,z)=0.

Координаты произвольной точки M(x;y;z) принадлежащей линии или поверхности, называются текущими координатами . Чтобы найти уравнение линии (поверхности), надо найти устойчивую, справедливую для всех точек связь между текущими координатами.

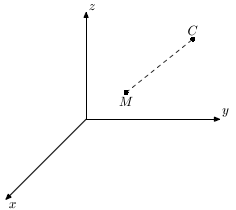
Пример. Найти уравнение множества S точек в пространстве переменных x, y, z, удаленных от точки C(x₀;y₀;z₀) на расстояние r - const (рис. 6.5).

Рис. 6.5. Геометрическое изображение свойства точек

Пусть M(x;y;z) - текущая точка множества S. По свойству точек этого множества S имеем: |CM|=r.

Так как в координатной форме можно записать вектор CM=({x-x₀} ; {y-y₀}; {z-z₀}), то получаем, что справедливо равенство вида:

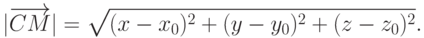
Из этого равенства получаем (x-x₀)² + (y-y₀)² + (z-z₀)² = r².

Мы нашли связь между координатами текущей точки M, то есть уравнение множества точек S в пространстве. Это уравнение определяет поверхность, называемую сферой. Любая точка M(x;y;z), удовлетворяющая этому уравнению, лежит на этой сфере. Отметим, что верхняя полусфера описывается уравнением

Если точка M(x;y;z) лежит внутри сферы, то ее координаты удовлетворяют неравенству |CM|² = (x-x₀)² + (y-y₀)² + (z-z₀)² < r².

Если точка M(x;y;z) лежит вне сферы, то ее координаты удовлетворяют неравенству вида: |CM|² = (x-x₀)² + (y-y₀)² + (z-z₀)² > r². Поэтому неравенство

Любая линия в пространстве может быть представлена как пересечение двух поверхностей. Если F₁(x,y,z)=0, F₂(x,y,z)=0 - уравнения двух поверхностей в пространстве, то система

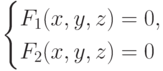
Пример. Линию пересечения двух сфер определяет система:

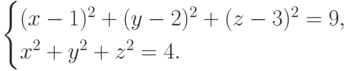
Для того чтобы найти на плоскости точки пересечения двух линий, заданных своими уравнениями f(x,y)=0, g(x,y)=0, необходимо решить систему из этих уравнений (так как эти точки должны лежать на каждой из этих линий, то есть удовлетворять уравнениям этих линий). Обратно, любое решение этой системы определяет точку пересечения линий.