|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Координаты и векторы
Численные величины подразделяются на скалярные (для которых важна лишь числовая характеристика) и векторные (для которых важна и ориентация).
Пример. Скорость автомобиля в некоторый определенный момент времени, количество студентов, словарный запас - скалярные величины. Скорость движения автомобиля (от начала до конца движения) - векторная величина.
Геометрическим вектором ( вектором ) называется направленный отрезок либо отрезок с указанием его ориентации на плоскости (плоскостной или двумерный вектор) или же в пространстве (пространственный вектор или трехмерный вектор). Он определяется парой точек - началом A и концом B и обозначается обычно как AB, a. Длина отрезка называется модулем вектора и обозначается |AB|, |a|. Это количественная характеристика вектора.
Если начало и конец вектора совпадают, то есть вектор вырождается в точку, то он называется нулевым .
Векторы a и b коллинеарны ( параллельны ), если они лежат на одной прямой или же на параллельных прямых, компланарны, если они лежат в одной плоскости или параллельно одной плоскости, и равны, если модули и направления этих векторов совпадают.
Угол  между векторами a и b обозначается как
между векторами a и b обозначается как 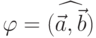 .
.
Радиус-вектор точки M(x;y) на плоскости Oxy или точки M(x;y;z) в пространстве Oxyz - это вектор OM .
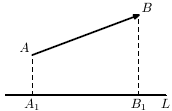
Пусть AB - произвольный вектор, A1, B1 - проекции точек A и B на некоторую ось L. Вектор A1B1 называется вектор-проекцией вектора AB .
Число |A1B1| называется проекцией AB на ось L (рис. 3.5). и обозначается  . Как легко заключить из чертежа, справедливы равенства |A1B1| = ПрLAB, |B1A1| = ПрLAB=|A1B1|.
. Как легко заключить из чертежа, справедливы равенства |A1B1| = ПрLAB, |B1A1| = ПрLAB=|A1B1|.
Спроецируем радиус-вектор OM на координатные оси Ox, Oy, Oz: x=Прx OM, y=Прy OM, z=Прz OM. Вектор OM с помощью этих проекций задается тройкой чисел OM={x, y, z}.
Пример. Если рассмотреть вектор a=(1; 2; -3), то его проекции на оси координат x, y, z будут равны, соответственно, 1, 2, -3.
Вектор единичной длины и направления, совпадающего с направлением координатной оси, называется единичным вектором или ортом этой оси.
Пусть i, j, k - орты осей Ox, Oy, Oz, то есть радиус-векторы точек Mx(1,0,0), My(0,1,0), Mz(0,0,1). Тогда |i| = |j| =|k| =1.
Теорема.
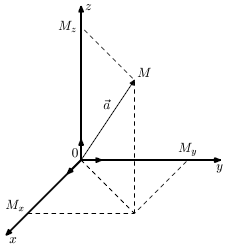
Любой вектор a может быть разложен по ортам осей
(рис. 3.6)., причем справедливо равенство 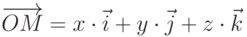 .
.
Последнее равенство называется разложением вектора по координатным осям, а числа x, y, z называют координатами вектора a.
Перейдем теперь от геометрического вектора к алгебраическому (математическому) вектору в его общей форме.
Вектором ( n -мерным) будем называть упорядоченный набор из n действительных чисел.Упорядоченность понимается в смысле указания порядка следования чисел друг за другом, то есть эти числа перенумерованы.
Записывается такой вектор в виде x=(x1,x2,...,xn) или x=(x1,...,xn). Число xi, i=1,2,...,n называется i -ой координатой вектора x , а число n - размерностью вектора.
Пример. Вектор a=(2) - одномерный вектор. Геометрически ему соответствует вектор (радиус-вектор) длины 2 и ориентированный в сторону положительного направления на числовой прямой. Вектор b=(-2) направлен в противоположную сторону и имеет длину 2. Вектор c=(7, -4) - двумерный вектор, геометрически ему соответствует вектор или радиус-вектор на плоскости с проекцией длины 7 на положительную полуось оси Ox и проекцией длины 4 на отрицательную полуось оси Oy. Вектор d=(-1, 2, 8) - трехмерный вектор, геометрически ему соответствует вектор или радиус-вектор в пространстве, x=(1, 3, -4, 6, 0) - пятимерный вектор, "геометрически" можно домыслить себе еще две координатные оси и тогда ему будет соответствовать радиус-вектор в пространстве пяти измерений.
Если два вектора, заданные в координатной форме, равны, то равны соответствующие координаты этих векторов, то есть справедливо x=(x1,...,xn) 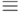 y=(y1,...,yn)
y=(y1,...,yn)  xi = yi i = 1, 2,..., n.
xi = yi i = 1, 2,..., n.
Вектор (0, 0, ..., 0) называется нулевым , обозначается 0, а векторы (1,0,...,0), (0,1,...,0), ..., (0,0,...,1) - единичными векторами, ортами .
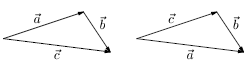
Суммой двух векторов a, b называется вектор c, c=a+b, начало которого совпадает с началом a, конец - с концом b, при условии, что начало b приложено к концу a .
Разностью двух векторов a и b называется вектор c, для которого c+b =a . Для его построения необходимо совместить концы уменьшаемого вектора a и вычитаемого b ; тогда начало c совпадает с началом a, а конец вектора c - с началом b (рис. 3.7).
Произведением вектора a на скаляр  называется вектор
называется вектор 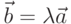 , который коллинеарен вектору a, направлен как
, который коллинеарен вектору a, направлен как 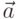 при
при 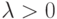 и в противоположную сторону при
и в противоположную сторону при  и имеет длину, равную
и имеет длину, равную  .
.
Все введенные операции справедливы для любых n-мерных векторов.