Основы "живого" моделирования

15.6. Сокращение вязкого тела с "выпучиванием"

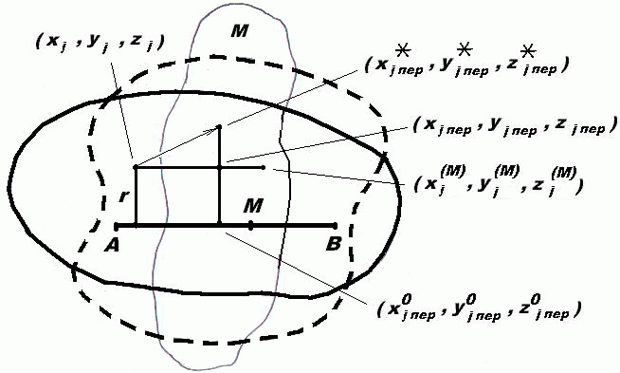
Сокращение вязкой и упругой среды, такой как резина, губка, упитанные щеки и др., обычно сопровождается явлением, которое можно назвать попыткой сохранения объема в результате выпучивания. При сокращении мышцы это означает, что перенос клеток объекта вдоль мышцы обретает перпендикулярную составляющую, тем меньшую, чем больше расстояние до мышцы.

Пусть, как и прежде, x_j, y_j, z_j — составляющие адрес координаты текущей клетки вязкого объекта, для которого выше сформированы выражения (15.8) для определения адреса переноса. Дополним их указанной перпендикулярной составляющей (рис. 15.5).

Рис. 15.5. Сокращение тела с "выпучиванием"

По (15.7), подставив вместо x_j0, y_j0, z_j0 значение найденной по (15.8) точки переноса (x_{j пер}, y _{j пер} , z_{j пер}) , найдем k_min и, невзирая на его значение, найдем проекцию (x_j⁰_пер, y_j⁰_пер, z_j⁰_пер) на мышцу или ее продолжение влево или вправо.

(Заметим, что уравнения (1) при 0 <= k <= 1 определяют собственно мышцу, другие значения определяют точки прямой, которой принадлежит отрезок — мышца.)

Запишем систему параметрических уравнений прямой, проходящей через точки (x_{j пер}, y _{j пер} , z_{j пер}) и (x_{j пер}⁰, y_{j пер}⁰, z_{j пер}⁰) :

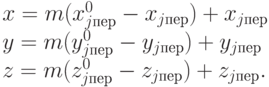( 15.9)

Задав малое приращение 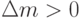, зависящее от r²_пер = (x_{j пер}⁰ - x_j)² + (y_{j пер}⁰ - y_j)² + (z_{j пер}⁰ - z_{j пер})² , и приняв 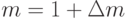, получим окончательно точку переноса (x_{j пер}*, y_{j пер}*, z_{j пер}*) , отстоящую от точки переноса, найденной по (15.8), и смещенную в перпендикулярном направлении от мышцы.

Эмпирическую зависимость коэффициента смещения от указанного выше расстояния можно выбрать как

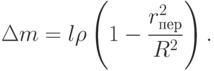( 15.10)

Тогда из (9) находим

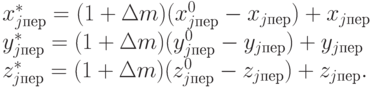( 15.11)

Таким образом, сокращая мышцу АВ, показанную на рис. 15.2, можно, например, изобразить то подобие улыбки, которая обозначена пунктиром. Введение других мышц, например, А₁В₁ под нижней губой, может значительно усилить правдоподобие улыбки.

15.7. Шарнирно-мышечное соединение

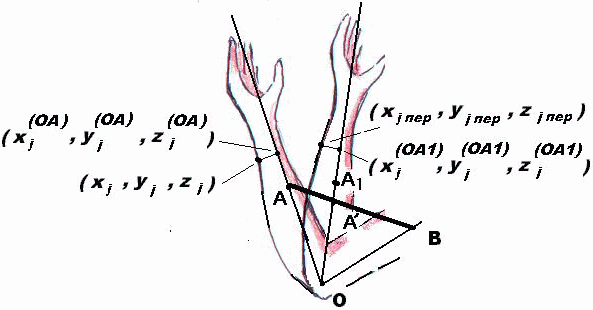
Координаты шарнира задаются условно (ячейка не занимается) точкой O(x₀, y₀, z₀) внутри объекта (рис. 15.6). Мышца АВ связывает лучи (элементы скелета), исходящие из точки О. Сокращение мышцы должно вызывать видимость движений, характерных при ходьбе, движении рук и т.д. Это требует таких деформаций объектов, при которых его клетки, облегающие эти лучи, или только клетки оболочки, несущие в себе данные лучи, сближаются вместе с лучами, не приводя к дополнительной деформации.

Рис. 15.6. Деформация объекта вокруг шарнира

Практический интерес представляет случай, когда неподвижная точка мышцы совпадает с одним из ее концов. Это соответствует направлению движения конечности относительно неподвижного тела. (Хотя следование известным соотношениям о количестве движения или третьего закона механики не представляет трудностей.)

По аналогии с (15.1), луч ОА описывается параметрической системой уравнений

( 15.12)

Если 0 <= k <= 1, то уравнения отображают отрезок ОА. Нас же интересует вся прямая, исходящая из точки О.

Отобразим сокращение мышцы переносом клетки А в клетку А' (x₁', y₁', z₁' ), в упрощенной форме воспользовавшись (15.2) и (15.3). Этим установим новое положение ОА' луча ОА.

Уравнения этого луча имеют вид

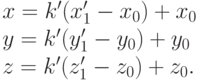( 15.13)

Если 0 <= k' <= 1, то уравнения отображают отрезок ОА'. Однако точка А' не отображает факт вращения луча ОА вокруг точки О. При этом вращении точка А должна переместиться в точку А₁ , отстоящую от О на расстояние, равное длине отрезка ОА. Найдем координаты этой точки на луче ОА' из соотношения

(x₁₁ - x₀)² + (y₁₁ - y₀)² + (z₁₁ - z₀)² = r² = (x₁ - x₀)² + (y₁ - y₀)² + (z₁ - z₀)².

В параметрической форме представления (12) точке (x₁₁, y₁₁, z₁₁) соответствует некоторое значение k₁' параметра. Подставим вместо координат этой точки их параметрическое представление:

(k₁')²((x₁' - x₀)² + (y₁' - y₀ )² + (z₁' - z₀)²) = r² .

Откуда

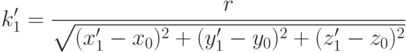( 15.14)

Очевидно, k₁' > 0 . Таким образом, точка А₁ переноса конца А мышцы найдена.

Для синхронных действий при переносе всех клеток объекта, подлежащих перемещению вокруг шарнира, запишем уравнения луча ОА₁ в зависимости от того же параметра k, определяющего положение (15.12) луча ОА

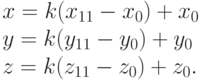( 15.15)

Пусть (x_j, y_j, z_j) — точка (клетка), подлежащая переносу, в соответствии с сокращением мышцы, в точку с тем же радиусом относительно точки О, но с исключением других деформаций объекта. Чтобы найти координаты (x_j^(OA), y_j^(OA), z_j^(OA)) проекции этой точки на луч ОА, решим задачу минимизации расстояния между этой точкой и лучом ОА, описанным системой (15.12):

(x_j - k(x₁ - x₀)- x₀)² + (y_j - k(y₁ - y₀) - y₀)² + (z_j - k(z₁ - z₀) - z₀)² -> min.

Приравняв производную по k нулю, получим

(x_j - k(x₁ - x₀) - x₀)(x₁ - x₀) + (y_j - k(y₁ - y₀) - y₀ )(y₁ - y₀) + (z_j - k(z₁ - z₀) - z₀)(z₁ - z₀) = 0.

Отсюда

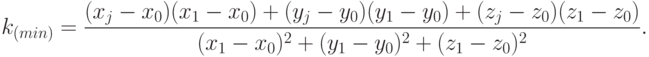( 15.16)

Подставим (15.16) в (15.12) и найдем координаты (x_j^(OA), y_j^(OA), z_j^(OA)) искомой проекции.

Вычислим разности координат точки (x_j, y_j, z_j) и найденной ее проекции на луч ОА, определяющие смещение этой точки:

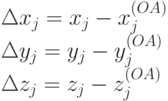( 15.17)

Подстановкой (15.15) в (15.14) найдем координаты (x_j^(OA1), y_j^OA1), z_j^(OA1)) "образа" точки (x_j^(OA), y_j^OA), z_j^(OA)) при повороте луча. Тогда координаты x _{j пер} , y_{j пер}, z_{j пер} переноса точки (x_j, y_j, z_j) отыскиваются так:

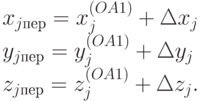( 15.18)

Организовав цикл по j - по всем точкам объекта (или оболочки) в окрестности луча ОА, выполним требуемую имитацию движения.