Развертки и граф-машина
Но вернемся к исследованию параллелизма с помощью разверток.
Изучение параллельной структуры алгоритмов связано с отысканием
множеств операций, которые можно выполнять независимо друг от друга. В
терминах, связанных с графом алгоритма, это эквивалентно нахождению
множеств его вершин, не связанных между собой ни дугами, ни путями
графа. Рассмотрим непересекающиеся множества 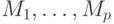 вершин графа
алгоритма
вершин графа
алгоритма  . Назовем эти множества параллельными по графу
. Назовем эти множества параллельными по графу  или просто
параллельными, если любой путь, связывающий две вершины одного
множества, целиком лежит в этом множестве и никакие две вершины из
разных множеств не связаны ни дугой, ни путем графа
или просто
параллельными, если любой путь, связывающий две вершины одного
множества, целиком лежит в этом множестве и никакие две вершины из
разных множеств не связаны ни дугой, ни путем графа  . Под
параллельной структурой алгоритма или графа будем понимать
совокупность сведений о параллельных множествах. Сюда же будем
относить и сведения о тех преобразованиях, целью которых является либо
выявление, либо изменение параллельных множеств. Говоря о
параллелизме, обычно обсуждают два его вида: макропараллелизм и
микропараллелизм. Макропараллелизм связан с ситуацией, когда все или
хотя бы часть из параллельных множеств содержат много точек.
Микропараллелизм имеет дело с теми случаями, при которых в каждом из
параллельных множеств находится всего лишь несколько точек. Типичной
для микропараллелизма является ситуация, когда все множества содержат
только по одной точке.
. Под
параллельной структурой алгоритма или графа будем понимать
совокупность сведений о параллельных множествах. Сюда же будем
относить и сведения о тех преобразованиях, целью которых является либо
выявление, либо изменение параллельных множеств. Говоря о
параллелизме, обычно обсуждают два его вида: макропараллелизм и
микропараллелизм. Макропараллелизм связан с ситуацией, когда все или
хотя бы часть из параллельных множеств содержат много точек.
Микропараллелизм имеет дело с теми случаями, при которых в каждом из
параллельных множеств находится всего лишь несколько точек. Типичной
для микропараллелизма является ситуация, когда все множества содержат
только по одной точке.
В ближайших рассмотрениях особый интерес будут представлять различные множества, образованные группами вершин, лежащих на поверхностях уровней разверток. Выделяются два типа разверток. Один тип составляют развертки, которые обеспечивают отсутствие связей внутри множеств. Это строгие развертки. Они дают возможность обнаружить в алгоритме микропараллелизм. Второй тип составляют развертки, которые обеспечивают отсутствие связей между множествами. Такие развертки называются расщепляющими. Они позволяют расщепить алгоритм на не связанные между собой фрагменты или, другими словами, позволяют обнаружить макропараллелизм.
Продемонстрируем подобное расщепление на примере использования
обобщенных разверток. Докажем сначала два полезных факта. Пусть для
графа алгоритма G построены обобщенные развертки 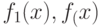 . Как
следует из определения разверток, функционал
. Как
следует из определения разверток, функционал 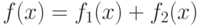 также
будет обобщенной разверткой. Рассмотрим какую-нибудь поверхность
уровня развертки
также
будет обобщенной разверткой. Рассмотрим какую-нибудь поверхность
уровня развертки  , содержащую не менее двух вершин-точек
, содержащую не менее двух вершин-точек 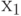 и
и  .
Допустим, что для этих точек
.
Допустим, что для этих точек  , но
, но  .
Предположим, например, что
.
Предположим, например, что  . Отсюда сразу же вытекает, что
. Отсюда сразу же вытекает, что 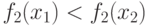 . Если точки связаны путем графа
. Если точки связаны путем графа  , то для любой развертки путь может идти лишь из точки с меньшим ее
значением в точку с большим значением. Поэтому заключаем, что точки
, то для любой развертки путь может идти лишь из точки с меньшим ее
значением в точку с большим значением. Поэтому заключаем, что точки  и
и  не могут быть связаны путем графа
не могут быть связаны путем графа  . Аналогичный вывод имеет
место и в случае предположения
. Аналогичный вывод имеет
место и в случае предположения 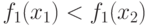 .
.
С другой стороны, при выполнении условий  и
и  будет также выполняться равенство
будет также выполняться равенство  .
Следовательно, точки
.
Следовательно, точки  из одной поверхности уровня развертки
из одной поверхности уровня развертки  будут находиться и на каких-то поверхностях уровней разверток
будут находиться и на каких-то поверхностях уровней разверток  и
и 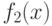 . Более того, при выполнении указанных равенств для любой пары
точек
. Более того, при выполнении указанных равенств для любой пары
точек 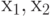 , принадлежащих любому фиксированному множеству из одной
поверхности уровня развертки
, принадлежащих любому фиксированному множеству из одной
поверхности уровня развертки  , все точки множества будут лежать на одной и той же поверхности уровня развертки
, все точки множества будут лежать на одной и той же поверхности уровня развертки  и на одной и той же
поверхности уровня развертки
и на одной и той же
поверхности уровня развертки 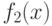 . Действительно, пусть в
рассматриваемом множестве имеется точка
. Действительно, пусть в
рассматриваемом множестве имеется точка  , отличная от точек
, отличная от точек  .
Тогда при выполнении условий
.
Тогда при выполнении условий  и
и 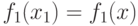 для пары точек
для пары точек 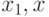 будет выполняться и равенство
будет выполняться и равенство 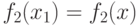 . Но значения
. Но значения 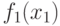 и
и 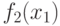 однозначно определяют поверхности уровней.
однозначно определяют поверхности уровней.
Конечно, в частном случае рассматриваемое множество может полностью
совпадать со всей поверхностью уровня. Предположим, что каждая
поверхность уровня развертки  содержится в какой-то поверхности
уровня развертки
содержится в какой-то поверхности
уровня развертки  или
или 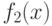 . Все три развертки относятся к одному
и тому же графу. Поэтому число всех вершин во всех поверхностях
уровней для каждой развертки будет одним и тем же. Отсюда вытекает,
что рассматриваемые как множества совокупности всех поверхностей
уровней разверток
. Все три развертки относятся к одному
и тому же графу. Поэтому число всех вершин во всех поверхностях
уровней для каждой развертки будет одним и тем же. Отсюда вытекает,
что рассматриваемые как множества совокупности всех поверхностей
уровней разверток 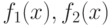 и
и  совпадают.
совпадают.
Пусть для графа алгоритма  построены обобщенные
развертки
построены обобщенные
развертки  , где
, где  .
Функционал
.
Функционал 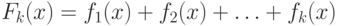 также будет
обобщенной разверткой при любом
также будет
обобщенной разверткой при любом  . Теперь по
развертке
. Теперь по
развертке  в соответствии с ее поверхностями уровней расщепим
множество вершин графа алгоритма на последовательно связанные между
собой группы. Возьмем далее развертку
в соответствии с ее поверхностями уровней расщепим
множество вершин графа алгоритма на последовательно связанные между
собой группы. Возьмем далее развертку 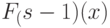 и в соответствии с ее
поверхностями уровней расщепим каждую из групп на подгруппы. Каждая из
подгрупп соответствует пересечению поверхностей уровней разверток
и в соответствии с ее
поверхностями уровней расщепим каждую из групп на подгруппы. Каждая из
подгрупп соответствует пересечению поверхностей уровней разверток  и
и  . Допустим, что на поверхности уровня развертки
. Допустим, что на поверхности уровня развертки  имеются такие точки
имеются такие точки 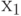 и
и 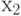 , что
, что  . Согласно
сказанному выше точки
. Согласно
сказанному выше точки 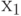 и
и  не могут быть связаны путем графа
не могут быть связаны путем графа  .
Вследствие условия
.
Вследствие условия  они заведомо принадлежат разным
подгруппам. По этой причине любые две точки
они заведомо принадлежат разным
подгруппам. По этой причине любые две точки 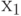 и
и  , взятые по одной
из этих двух подгрупп, не могут удовлетворять условию
, взятые по одной
из этих двух подгрупп, не могут удовлетворять условию  .
Поэтому подгруппы оказываются параллельными.
.
Поэтому подгруппы оказываются параллельными.
Если на каждой поверхности уровня развертки  для любой пары
точек
для любой пары
точек  и
и 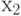 будет выполняться равенство
будет выполняться равенство  , то в
соответствии со сказанным ранее это означает, что поверхности уровней
разверток
, то в
соответствии со сказанным ранее это означает, что поверхности уровней
разверток  и
и  совпадают. Следовательно, по сравнению
с набором разверток
совпадают. Следовательно, по сравнению
с набором разверток  развертка
развертка  не
добавляет новой информации в отношении распределения вершин-точек
графа по поверхностям уровней и ее можно исключить из рассмотрения. В
случае успешного использования развертки
не
добавляет новой информации в отношении распределения вершин-точек
графа по поверхностям уровней и ее можно исключить из рассмотрения. В
случае успешного использования развертки  далее пытаемся
расщепить подгруппы на параллельные множества с помощью развертки
далее пытаемся
расщепить подгруппы на параллельные множества с помощью развертки  и т.д.
и т.д.
Заметим, что сейчас не идет речь о поиске наилучших в каком-либо смысле параллельных множеств. Демонстрируется лишь возможность использования обобщенных разверток для обнаружения какого-то параллелизма.
Вообще говоря, развертки устроены достаточно сложно. Множество обобщенных разверток замкнуто в отношении некоторых операций над ними. Из определения разверток можно заключить, что обобщенной разверткой является
- сумма обобщенных разверток,
- произведение обобщенной развертки на неотрицательное число,
- максимум из обобщенных разверток,
- минимум из обобщенных разверток.
Можно также показать, что в отношении трех последних операций множество обобщенных разверток представляет полумодуль. В нем существуют "нулевая" и "единичная" развертка, а также "оптимальная" развертка, обеспечивающая реализацию алгоритма за минимальное время при наличии ограничений снизу на времена выполнения операций и времена передачи данных. Различные нетривиальные свойства разверток описаны в [ 1 ] и приведенной там литературе.
Будем по-прежнему считать, что граф алгоритма расположен в арифметическом пространстве X подходящей размерности. В этом случае без ограничения общности дуги графа можно рассматривать как векторы. С практической точки зрения целесообразно использовать самые простые развертки. Развертка задается функционалом, определенным на конечном множестве вершин-точек. Тем не менее, ничто не мешает рассматривать любые подходящие расширения функционалов на все пространство X. Ясно, что в первую очередь следует изучить возможность использования линейных функционалов.
Пусть векторы 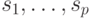 описывают множество дуг графа.
Предположим, что для некоторого вектора
описывают множество дуг графа.
Предположим, что для некоторого вектора  выполняются условия
выполняются условия 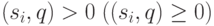 для всех
для всех  .
Будем называть граф строго направленным
(направленным) относительно вектора
.
Будем называть граф строго направленным
(направленным) относительно вектора  , а сам вектор
, а сам вектор  - строго
направляющим (направляющим) вектором графа. Рассмотрим в пространстве
- строго
направляющим (направляющим) вектором графа. Рассмотрим в пространстве  линейный функционал
линейный функционал 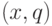 и его поверхности уровней
и его поверхности уровней 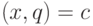 для
различных значений константы
для
различных значений константы  . Если дуга
. Если дуга  графа идет из вершины
графа идет из вершины  в
вершину
в
вершину  , то
, то 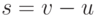 . Согласно определению, для строго направленного
(направленного) относительно вектора
. Согласно определению, для строго направленного
(направленного) относительно вектора  графа должно выполняться
неравенство
графа должно выполняться
неравенство 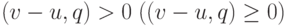 или
или 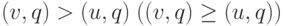 .
Поэтому для строго направленного (направленного) относительно вектора
.
Поэтому для строго направленного (направленного) относительно вектора  графа функционал
графа функционал 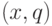 определяет строгую (обобщенную) развертку.
Развертки вида
определяет строгую (обобщенную) развертку.
Развертки вида 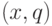 будем называть линейными.
будем называть линейными.
Уравнения 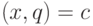 при разных значениях
при разных значениях  задают в
задают в  некоторое
семейство гиперплоскостей. По отношению к дугам графа это семейство
обладает важными свойствами, которые нагляднее всего описать
геометрически. Именно, для строго направленного графа дуги могут
проходить через любую гиперплоскость только из отрицательного
(неположительного) полупространства в неотрицательное (положительное)
полупространство. Никакие дуги не могут лежать на самой
гиперплоскости, поскольку вершины графа на гиперплоскости представляют
не что иное как поверхность уровня развертки
некоторое
семейство гиперплоскостей. По отношению к дугам графа это семейство
обладает важными свойствами, которые нагляднее всего описать
геометрически. Именно, для строго направленного графа дуги могут
проходить через любую гиперплоскость только из отрицательного
(неположительного) полупространства в неотрицательное (положительное)
полупространство. Никакие дуги не могут лежать на самой
гиперплоскости, поскольку вершины графа на гиперплоскости представляют
не что иное как поверхность уровня развертки 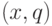 . Для направленного
графа дуги могут проходить через гиперплоскость только из
неположительного полупространства в неотрицательное полупространство.
Какие-то дуги могут лежать на гиперплоскости. Но ни для какого
направленного графа дуги не могут пересекать ни одну гиперплоскость в противоположных направлениях. Единственное, что допускается, - это
нахождение каких-то дуг на каких-то гиперплоскостях и только для
графа, направленного не строго относительно вектора
. Для направленного
графа дуги могут проходить через гиперплоскость только из
неположительного полупространства в неотрицательное полупространство.
Какие-то дуги могут лежать на гиперплоскости. Но ни для какого
направленного графа дуги не могут пересекать ни одну гиперплоскость в противоположных направлениях. Единственное, что допускается, - это
нахождение каких-то дуг на каких-то гиперплоскостях и только для
графа, направленного не строго относительно вектора  .
.
Выберем возрастающую последовательность чисел 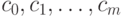 . Будем
считать для определенности, что в отрицательном (неотрицательном)
полупространстве гиперплоскости
. Будем
считать для определенности, что в отрицательном (неотрицательном)
полупространстве гиперплоскости 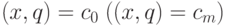 нет ни одной
вершины графа, а в каждом из полуслоев
нет ни одной
вершины графа, а в каждом из полуслоев 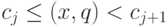 для всех
для всех  , имеется хотя бы по одной вершине. С позиций макровычислений
полуслои похожи на "толстые" поверхности уровней обобщенных
разверток. Допустим, что дуга связывает две вершины из разных
полуслоев. Если
, имеется хотя бы по одной вершине. С позиций макровычислений
полуслои похожи на "толстые" поверхности уровней обобщенных
разверток. Допустим, что дуга связывает две вершины из разных
полуслоев. Если  считать номером полуслоя, то любая дуга
может идти лишь из полуслоя с меньшим номером в полуслой с большим
номером. Это тривиальное замечание вскоре будет эффектно использовано.
Очевидно, что соответствующие полуслоям операции алгоритма можно
выполнять последовательно полуслой за полуслоем согласно росту
номера
считать номером полуслоя, то любая дуга
может идти лишь из полуслоя с меньшим номером в полуслой с большим
номером. Это тривиальное замечание вскоре будет эффектно использовано.
Очевидно, что соответствующие полуслоям операции алгоритма можно
выполнять последовательно полуслой за полуслоем согласно росту
номера  .
.
Пусть снова векторы 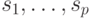 описывают все множество дуг графа.
Но теперь предположим, что для графа найдено
описывают все множество дуг графа.
Но теперь предположим, что для графа найдено 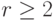 линейно независимых
векторов
линейно независимых
векторов 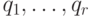 , строгой или нестрогой направленности. Для всех
, строгой или нестрогой направленности. Для всех 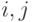 построим по описанным только что правилам гиперплоскости
построим по описанным только что правилам гиперплоскости 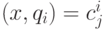 и
полуслои
и
полуслои 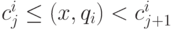 . Перенумеруем относящиеся к векторам
. Перенумеруем относящиеся к векторам  полуслои подряд натуральными числами
полуслои подряд натуральными числами 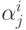 , в соответствии с ростом
номеров
, в соответствии с ростом
номеров  . Пересечение любых
. Пересечение любых  полуслоев, соответствующих разным
векторам
полуслоев, соответствующих разным
векторам  представляет полуоткрытый параллелепипед. Поэтому все
вершины графа оказываются распределенными по некоторой r -мерной
системе непересекающихся полуоткрытых параллелепипедов, гранями
которых являются построенные гиперплоскости. Внутри каждого
параллелепипеда расположен некоторый подграф, описывающий какой-то
фрагмент алгоритма. Тем самым получено разбиение на отдельные
фрагменты всего алгоритма. Основной вопрос заключается в том, возможно
ли правильно реализовать алгоритм в целом, выполняя в каком-либо
порядке отдельные его фрагменты, и если возможно, то как это
делать?
представляет полуоткрытый параллелепипед. Поэтому все
вершины графа оказываются распределенными по некоторой r -мерной
системе непересекающихся полуоткрытых параллелепипедов, гранями
которых являются построенные гиперплоскости. Внутри каждого
параллелепипеда расположен некоторый подграф, описывающий какой-то
фрагмент алгоритма. Тем самым получено разбиение на отдельные
фрагменты всего алгоритма. Основной вопрос заключается в том, возможно
ли правильно реализовать алгоритм в целом, выполняя в каком-либо
порядке отдельные его фрагменты, и если возможно, то как это
делать?
Каждый параллелепипед однозначно характеризуется r -мерной
совокупностью своих номеров 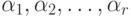 . Рассмотрим два
параллелепипеда с номерами
. Рассмотрим два
параллелепипеда с номерами 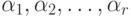 и
и 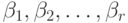 . По
построению, дуга из первого параллелепипеда может идти во второй
только в том случае, когда для всех
. По
построению, дуга из первого параллелепипеда может идти во второй
только в том случае, когда для всех 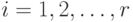 выполняются
нестрогие неравенства
выполняются
нестрогие неравенства  , и хотя бы для одного значения
, и хотя бы для одного значения  ,
например, равного
,
например, равного  , имеет место строгое неравенство
, имеет место строгое неравенство  .
Просуммировав почленно все эти неравенства, заключаем, что необходимо
должно выполняться суммарное неравенство
.
Просуммировав почленно все эти неравенства, заключаем, что необходимо
должно выполняться суммарное неравенство  .
Разобьем параллелепипеды на группы, относя к одной группе те и только
те из них, которые будут иметь одинаковые суммы номеров
.
Разобьем параллелепипеды на группы, относя к одной группе те и только
те из них, которые будут иметь одинаковые суммы номеров 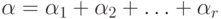 .
Как вытекает из суммарного неравенства, в одной группе
не могут существовать параллелепипеды, связанные между собой дугами
графа. Из него же следует, что дуга не может идти из параллелепипеда с
большей суммой номеров в параллелепипед с меньшей суммой номеров.
Упорядочим группы по росту суммы номеров, начиная с
.
Как вытекает из суммарного неравенства, в одной группе
не могут существовать параллелепипеды, связанные между собой дугами
графа. Из него же следует, что дуга не может идти из параллелепипеда с
большей суммой номеров в параллелепипед с меньшей суммой номеров.
Упорядочим группы по росту суммы номеров, начиная с 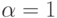 . Возможно,
некоторые из групп окажутся пустыми. Однако это не мешает выполнять
группы фрагментов последовательно друг за другом в порядке роста суммы
номеров. Внутри же каждой группы фрагменты не связаны между собой и их
можно выполнять параллельно.
. Возможно,
некоторые из групп окажутся пустыми. Однако это не мешает выполнять
группы фрагментов последовательно друг за другом в порядке роста суммы
номеров. Внутри же каждой группы фрагменты не связаны между собой и их
можно выполнять параллельно.
Итак, знание хотя бы двух независимых линейных разверток, причем не обязательно строгих, позволяет перейти от описания алгоритма в терминах исходных операций к описанию того же алгоритма, но уже в терминах его фрагментов или, другими словами, в терминах более крупных макроопераций. Для макроописания алгоритма легко находится параллельная форма. Чем больше известно независимых разверток, тем больше ширина ярусов у этой параллельной формы. Но чем больше ширина ярусов, тем больше параллелизма удается выявить в алгоритме. С этой точки зрения наиболее интересным является случай, когда число известных разверток совпадает с размерностью того пространства, в котором размещен граф алгоритма.
Пусть граф является строго направленным относительно какого-то
вектора  . Из соображений непрерывности ясно, что всегда можно найти
полный базис близких к
. Из соображений непрерывности ясно, что всегда можно найти
полный базис близких к  векторов, по отношению к которым граф также
является строго направленным. Однако их прямое использование не всегда
бывает целесообразным или даже становится невозможным. Если среди дуг
графа много таких, которые близки к ортогональным по отношению к
вектору
векторов, по отношению к которым граф также
является строго направленным. Однако их прямое использование не всегда
бывает целесообразным или даже становится невозможным. Если среди дуг
графа много таких, которые близки к ортогональным по отношению к
вектору  , то это приводит к появлению сильно сжатых вдоль вектора
, то это приводит к появлению сильно сжатых вдоль вектора  параллелепипедов. Нередко такое сжатие оказывается тем сильнее, чем
больше сам граф, что, в свою очередь, влечет за собой большие
вычислительные и организационные трудности в реализации макроопераций.
На практике более удобно иметь дело с направляющими векторами,
близкими к ортогональным между собой, даже если по отношению к ним
графы направлены и не строго.
параллелепипедов. Нередко такое сжатие оказывается тем сильнее, чем
больше сам граф, что, в свою очередь, влечет за собой большие
вычислительные и организационные трудности в реализации макроопераций.
На практике более удобно иметь дело с направляющими векторами,
близкими к ортогональным между собой, даже если по отношению к ним
графы направлены и не строго.
Очень важно, что размеры всех макроопераций можно регулировать за счет выбора "толщины" полуслоев. Предположим, что макрооперации реализуются на отдельных процессорах многопроцессорной вычислительной системы. В общем случае, при увеличении параллелепипеда количество попавших в него операций алгоритма, т.е. время реализации макрооперации, растет как объем параллелепипеда. Количество же связей с другими макрооперациями, т.е. количество дуг, пересекающих грани параллелепипеда, растет как площадь его поверхности. Объем растет быстрее площади поверхности. Поэтому при увеличении макроопераций полезная загруженность процессоров будет увеличиваться, поскольку на выполнение собственно самих операций будет тратиться относительно больше времени, чем на обмен информацией с другими процессорами.
Одним из самых интересных классов алгоритмов, графы которых
оказываются направленными, являются рекуррентные соотношения.
Рассмотрим конечномерное пространство целочисленных вектор-индексов  с лексикографическим порядком и в нем непустую область
с лексикографическим порядком и в нем непустую область  . Соотношения
вида
. Соотношения
вида
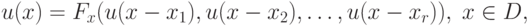
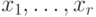 фиксированы, целочисленные и не зависят от
фиксированы, целочисленные и не зависят от  . Функции
. Функции  могут быть произвольными, в том числе как линейными, так
и нелинейными. Выполняются эти соотношения в порядке
лексикографического роста вектор-индекса
могут быть произвольными, в том числе как линейными, так
и нелинейными. Выполняются эти соотношения в порядке
лексикографического роста вектор-индекса  . Если какой-либо из
векторов
. Если какой-либо из
векторов  не принадлежит области
не принадлежит области  , то соответствующая переменная
, то соответствующая переменная  считается заданной и представляет одно из входных данных
алгоритма.
считается заданной и представляет одно из входных данных
алгоритма.Будем размещать вершины графа алгоритма в точках области  с
целочисленными координатами. Вершине, задаваемой вектором
с
целочисленными координатами. Вершине, задаваемой вектором  , поставим
в соответствие функцию
, поставим
в соответствие функцию  . Если
. Если  , то из рекуррентных соотношений
вытекает, что в вершину
, то из рекуррентных соотношений
вытекает, что в вершину  будут входить дуги из вершин
будут входить дуги из вершин 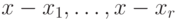 и только из этих вершин. В случае, когда какой-то из векторов
и только из этих вершин. В случае, когда какой-то из векторов  не
принадлежит области
не
принадлежит области  , вектор
, вектор  будет символизировать функцию ввода
переменной
будет символизировать функцию ввода
переменной 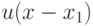 . Построенный таким образом граф имеет очень простую
структуру. Если дуги задавать векторами, то в каждую вершину из
области
. Построенный таким образом граф имеет очень простую
структуру. Если дуги задавать векторами, то в каждую вершину из
области  будет входить один и тот же пучок дуг, который переносится
параллельно от одной вершины к другой. Графы подобного вида называются регулярными, а образующие их векторы
будет входить один и тот же пучок дуг, который переносится
параллельно от одной вершины к другой. Графы подобного вида называются регулярными, а образующие их векторы 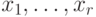 - базовыми. Заметим,
что при других размещениях вершин графа алгоритма регулярная структура
дуг может нарушаться. Данный пример наглядно подтверждает важность
согласования формы записи алгоритма с формой представления его
графа.
- базовыми. Заметим,
что при других размещениях вершин графа алгоритма регулярная структура
дуг может нарушаться. Данный пример наглядно подтверждает важность
согласования формы записи алгоритма с формой представления его
графа.
Регулярные графы совсем не обязательно связывать с рекуррентными
соотношениями. Важно лишь, чтобы вершины графов располагались в точках
с целочисленными координатами. Тогда сами графы можно строить, просто
перенося пучок заданных базовых векторов 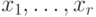 от одной вершины к
другой. В общем случае такие графы могут иметь контуры, т.е. не быть
графами никаких алгоритмов. Однако доказано
[
1
]
, что регулярный граф,
вершины которого расположены в точках с целочисленными координатами,
не имеет контуры тогда и только тогда, когда существует вектор
от одной вершины к
другой. В общем случае такие графы могут иметь контуры, т.е. не быть
графами никаких алгоритмов. Однако доказано
[
1
]
, что регулярный граф,
вершины которого расположены в точках с целочисленными координатами,
не имеет контуры тогда и только тогда, когда существует вектор  ,
относительно которого граф является строго направленным. Не
ограничивая общности, вектор
,
относительно которого граф является строго направленным. Не
ограничивая общности, вектор  можно считать целочисленным. Поскольку
все дуги графа описываются базовыми векторами
можно считать целочисленным. Поскольку
все дуги графа описываются базовыми векторами 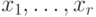 , то должны
выполняться строгие неравенства
, то должны
выполняться строгие неравенства 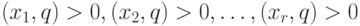 . В
этом случае заведомо существует столько строгих независимых линейных
разверток, какова размерность линейной оболочки векторов
. В
этом случае заведомо существует столько строгих независимых линейных
разверток, какова размерность линейной оболочки векторов 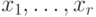 .
Тем не менее, как уже отмечалось, использовать их можно лишь с
определенной осторожностью. С практической точки зрения во многих
случаях удобнее брать линейные обобщенные развертки, направляющие
векторы которых совпадают с направляющими векторами граней выпуклого
конуса, образованными векторами
.
Тем не менее, как уже отмечалось, использовать их можно лишь с
определенной осторожностью. С практической точки зрения во многих
случаях удобнее брать линейные обобщенные развертки, направляющие
векторы которых совпадают с направляющими векторами граней выпуклого
конуса, образованными векторами 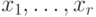 . В силу целочисленности
координат базовых векторов, направляющие векторы разверток всегда
можно выбрать целочисленными.
. В силу целочисленности
координат базовых векторов, направляющие векторы разверток всегда
можно выбрать целочисленными.
Допустим, что для регулярного графа найдена линейная развертка 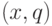 с целочисленным вектором
с целочисленным вектором  . Так как вершины графа расположены в
точках с целочисленными координатами, то уравнение любой поверхности
уровня
. Так как вершины графа расположены в
точках с целочисленными координатами, то уравнение любой поверхности
уровня 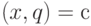 есть уравнение гиперплоскости с целыми коэффициентами.
Очевидно, что граф покрывается конечной системой таких
гиперплоскостей. Расстояние между соседними гиперплоскостями не
меньше, чем
есть уравнение гиперплоскости с целыми коэффициентами.
Очевидно, что граф покрывается конечной системой таких
гиперплоскостей. Расстояние между соседними гиперплоскостями не
меньше, чем 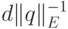 , где
, где  - наибольший общий делитель модулей
ненулевых координат вектора
- наибольший общий делитель модулей
ненулевых координат вектора  , -
евклидова норма вектора
[
1
]
.
Желание минимизировать время реализации алгоритма приводит к
минимизации числа гиперплоскостей, покрывающих граф. Если не принимать
во внимание частные особенности графов, то вектор
, -
евклидова норма вектора
[
1
]
.
Желание минимизировать время реализации алгоритма приводит к
минимизации числа гиперплоскостей, покрывающих граф. Если не принимать
во внимание частные особенности графов, то вектор  следует выбирать
так, чтобы величина
следует выбирать
так, чтобы величина 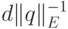 была максимальной.
была максимальной.
