|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Теоретические сведения о компьютерных вирусах
Результат Леонарда Адельмана
Леонард Адельман, известный математик, обладатель премии Тьюринга, участвовавший в свое время разработке криптосистемы RSA (буква A в аббревиатуре) для исследования феномена вирусов решил использовать другой формализм теории алгоритмов - не формализм машин Тьюринга, а формализм рекурсивных функций.
Теория машин Тьюринга и теория рекурсивных функций в некотором смысле эквиваленты - алгоритмы, вычислимые в одной теории будут вычислимыми в другой, и наоборот. Этот факт в совокупности с тезисом Тьюринга-Черча, означает, что полученные Л. Адельманом результаты в той же степени применимы к современным реалиям, что и результаты Ф. Коэна, Д. Чесса, С. Вайта, Ф. Лейтольда и других исследователей опиравшихся в своих работах на теорию машин Тьюринга.
Принятые обозначения
В дальнейшем изложении будет считаться, что данные и программы, во-первых, различимы, как это обычно и бывает в компьютерных системах, а во-вторых, могут быть закодированы натуральными числами. Поскольку и данные и программы всегда имеют ограниченный размер и ограниченный алфавит для их представления, принципиальная возможность взаимно однозначного кодирования натуральными числами сомнений не вызывает.
Исходя из сказанного, состояние некой вычислительной системы с точки зрения выполняющейся программы, может быть описано как набор доступных программе данных и других программ, что может быть выражено как наборы или последовательности натуральных чисел. Действие любой программы заключается в том, чтобы из одного набора данных и программ получить другой набор данных и программ.
Ниже везде неявно подразумевается описанная интерпретация вычислительной системы.
- Обозначим S - множество всех конечных последовательностей натуральных чисел,
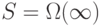 .
Таким образом элемент S может обозначать либо набор файлов данных, либо набор файлов программ,
закодированных при помощи натуральных чисел.
.
Таким образом элемент S может обозначать либо набор файлов данных, либо набор файлов программ,
закодированных при помощи натуральных чисел. - Обозначим e - вычислимую инъективную функцию из SxS на
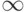 с вычислимой обратной функцией,
с вычислимой обратной функцией, 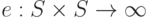 .
По тому же принципу, что и программы и данные, натуральными числами могут кодироваться и
состояния системы. Функция e взаимно однозначно ставит в соответствие набору данных и программ
натуральное число. Иными словами e - однозначная нумерация состояний системы.
.
По тому же принципу, что и программы и данные, натуральными числами могут кодироваться и
состояния системы. Функция e взаимно однозначно ставит в соответствие набору данных и программ
натуральное число. Иными словами e - однозначная нумерация состояний системы. -
Нотация
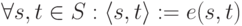
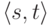 предназначена для обозначения состояния системы и фактически является
кодом этого состояния, представленным натуральным числом.
предназначена для обозначения состояния системы и фактически является
кодом этого состояния, представленным натуральным числом. - Для всех частичных функций
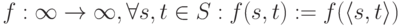 Любая программа переводит систему из одного состояния в другое, учитывая, что состояния кодируются
натуральными числами, можно считать любую программу функцией из
Любая программа переводит систему из одного состояния в другое, учитывая, что состояния кодируются
натуральными числами, можно считать любую программу функцией из 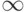 в
в 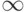 .
. - Для всех частичных функций
 примем обозначение
примем обозначение 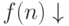 f(n) определена
f(n) определена - Для всех частичных функций
 примем обозначение
примем обозначение 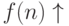 f(n) не определена
f(n) не определена
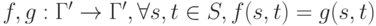 выполняется одно из условий:
выполняется одно из условий:-
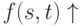 и
и 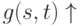 , либо
, либо -
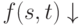 и
и 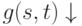 и f(s,t) = g(s,t)
и f(s,t) = g(s,t)
Определение служит для уточнения понятия тождественности программ, представленных в виде частичных функций.
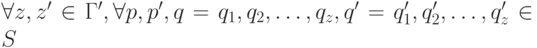 для всех частичных функций : :
для всех частичных функций : : 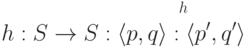
- z=z', и
- p=p', и
-
![\exists i \in [l,z]: q_i \ne q'_i](/sites/default/files/tex_cache/3d272cfcc2d34fde71c34ab8b302de5a.png) , и
, и -
![\forall i \in [l,z]](/sites/default/files/tex_cache/98b61b5fadf80ea8cab8460d52aa2065.png) либо
либо- q=q', либо
-
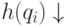 и h(qi)=q'i
и h(qi)=q'i
Если раньше для обозначения действия программы на систему использовались коды состояний, то в этом определении используется детализированное описание состояния и по сути вводится отношение между чистым и зараженным состоянием системы. Зараженное состояние характеризуется тем, что при прочих равных в нем некоторые программы изменены вирусом (функция h ).
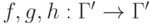 ,
, 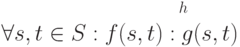
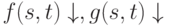 , и
, и 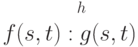
В этом определении уточняется введенное ранее отношение для состояний, получаемых
в результате действия двух функций. Результатом действия функции f на состояние системы 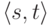 является натуральное число, которое можно однозначно
интерпретировать как новое состояние
является натуральное число, которое можно однозначно
интерпретировать как новое состояние  .
Точно так же
.
Точно так же 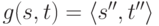 . Соответственно, запись
. Соответственно, запись 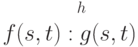 обозначает, что обе программы завершают свою работу при запуске из состояния
обозначает, что обе программы завершают свою работу при запуске из состояния 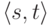 и результат их выполнения будет отличаться фактом заражения некоторых программ:
и результат их выполнения будет отличаться фактом заражения некоторых программ: 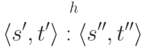 .
.
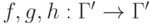 ,
, 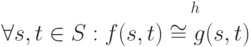
 или
или 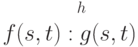
Введенное обозначение призвано отразить тот факт, что зараженная программа не всегда выполняет заражение - в некоторых состояниях зараженная программа может выполнять ровно те же действия, что и незараженная, т. е. результат ее действия при некоторых состояниях системы будут точно таким же как и у незараженной программы.
 ,
общерекурсивная функция v будет вирусом по отношению к
,
общерекурсивная функция v будет вирусом по отношению к 
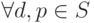 выполняется либо:
выполняется либо:- Повреждение:
![(\forall i,j \in \Gamma ')[\phi_{v(i)} (d,p) = \phi_{v(j)} (d,p)]](/sites/default/files/tex_cache/4e77cde06fb442c8ffd0ea821601d8b7.png)
- Заражение или имитация:
![\begin{aligned}
_v_~~~~~~~~~~~~~~~ \\
(\forall j \in \Gamma ')[\phi_j (d,p) \cong \phi_{v(j)} (d,p)]
\end{aligned}](/sites/default/files/tex_cache/d6f5d2fada1e0a971937950f59ac339f.png)
В данном определении выбор переменных d и p в явном виде указывает на их природу - данные (информация не подверженная заражению) и программы (информация подверженная заражению).
Здесь необходимы комментарии:
- Повреждение. Из определения следует, что результат действия зараженной программы при определенном состоянии системы определяется только типом вируса и состоянием системы, независимо от того, какая программа была заражена. На самом деле, выполняемое вирусом действие может и не быть деструктивным, важно то, что оригинальная программа не выполняется вовсе, т. е. выполняется функция прописанная в самом вирусе.
- Заражение или имитация. Здесь, согласно определению, ситуация прямо противоположная. Результат действия зараженной программы либо вовсе не отличается от результата действия исходной, либо отличается появлением в системе новых зараженных программ. Различное поведение определяется различиями в исходном состоянии системы.
Классификация вирусов
 ,
для всех вирусов v по отношению к
,
для всех вирусов v по отношению к 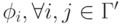 :
:-
i вредоносна по отношению к v и j
- i = v(j)
![\begin{aligned}
_v_~~~~~~~~~~~ \\
(\exists d,p \in S)[\phi_j (d,p) \not\cong \phi_i (d,p)]
\end{aligned}](/sites/default/files/tex_cache/05ddf5e13cee348221f681abe2f7ffdc.png)
Существует состояние системы, при котором зараженная вирусом v программа j выполняет вредоносную функцию, т.е. результат действия зараженной программы не ограничивается заражением (появлением новых зараженных программ).
-
i заразна по отношению к v и j
- i = v(j)
![\begin{aligned}
_v_~~~~~~~~~~ \\
(\exists d,p \in S)[\phi_j (d,p) : \phi_i (d,p)]
\end{aligned}](/sites/default/files/tex_cache/5289bf241f516bd3a8aa5f64d842f0f6.png)
Существует состояние системы, при котором зараженная вирусом v программа j выполняет функцию размножения - в результате ее действия в системе появляются новые зараженные программы.
-
i безобидна по отношению к v и j
- i = v(j)
- i не вредоносна по отношению к j
- i не заразна по отношению к j
-
i является трояном по отношению к v и j
- i = v(j)
- вредоносна по отношению к j
- i не заразна по отношению к j
Троян способен только к выполнению вредоносных функций и не может размножаться.
-
i является переносчиком по отношению к v и j
- i = v(j)
- не вредоносна по отношению к j
- i заразна по отношению к j
Переносчик является антиподом трояна: он только размножается и не содержит вредоносных функций.
-
i является вирусом по отношению к v и j
- i = v(j)
- i вредоносна по отношению к j
- i заразна по отношению к j
Вирус - наиболее универсальный тип вредоносных программ, способный как к размножению, так и к выполнению вредоносных действий.
В тех случаях когда существует единственная j такая, что (т.е. когда v инъективна) и i является вредоносной (заразной, безобидной, трояном, переносчиком, вирусом) по отношению к v и j, ссылка на j будет опускаться и i будет называться вредоносной (заразной, безобидной, трояном, переносчиком, вирусом) по отношению к v.
Таким образом, если по отношению к какому-либо вирусу инфицированная программа является безобидной, это значит что она выполняет в точности те же действия, что и исходная неинфицированная программа и никаких других. Если она является трояном, значит она не может заражать другие программы, а может только имитировать их действия или наносить вред. Если программа является переносчиком, значит она не способна наносить вред, но при определенных обстоятельствах может заражать другие программы.
 ,
для всех вирусов v по отношению к
,
для всех вирусов v по отношению к  :
:- вирус v безобиден одновременно справедливо:
- вирус v - троянский конь одновременно справедливо:
- вирус v только распространяется одновременно справедливо:
- вирус v вредоносен одновременно справедливо:
Следующая теорема отмечает ряд простых свойств, присущих различным типам вирусов.
 ,
для всех вирусов v по отношению к
,
для всех вирусов v по отношению к  :
:-
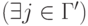 [v(j) безобидна по отношению к v и j]
[v(j) безобидна по отношению к v и j]
- вирус v безобиден
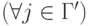 [v(j) безобидна по отношению к v и j]
[v(j) безобидна по отношению к v и j]
- если v - троян, то
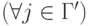 [v(j) безобидна по отношению к v и j]
или [v(j) является трояном по отношению к v и j]
[v(j) безобидна по отношению к v и j]
или [v(j) является трояном по отношению к v и j]
- если v способен только распространяться, то
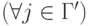 [v(j) безобидна по отношению к v и j]
или [v(j) является переносчиком по отношению к v и j]
[v(j) безобидна по отношению к v и j]
или [v(j) является переносчиком по отношению к v и j]
Доказательство. Первое свойство непосредственно следует из первой теоремы о рекурсии (теоремы о неподвижной точке).
Остальные свойства следует непосредственно из определений.
Обнаружение компьютерных вирусов
После определения компьютерного вируса естественным образом возникает вопрос об обнаружении такого рода программ, или о разрешимости множества компьютерных вирусов. Л. Адельман доказал следующую теорему.
Теорема приводится без доказательства.
Здесь 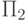 - класс множеств в арифметической классификации. Известно, что классы
множеств
- класс множеств в арифметической классификации. Известно, что классы
множеств 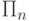 с индексом 1 и выше являются неразрешимыми. Следовательно и множество
вирусов является неразрешимым.
с индексом 1 и выше являются неразрешимыми. Следовательно и множество
вирусов является неразрешимым.
Заключение
Из вышеизложенного видно, что разные исследователи в разное время используя различный математический аппарат получили эквивалентный вывод. Класс вирусов является неразрешимым, т.е. не существует алгоритма, который бы позволил однозначно определить является программа зараженной (вирусом) или нет. Речь идет даже не о нехватке ресурсов, а о принципиальной невозможности создать подобный алгоритм.
В связи с этим проблема естественным образом переходит из теоретической области в практическую, где применяются частные решения для решения частных задач обнаружения вирусов. В частности решаются задачи определения вирусов по сигнатурам, или вероятностного определения вирусов. О подклассах вредоносных программ и практических методах борьбы с ними и пойдет речь в последующих главах.

![(\forall j \in \Gamma ') [v(j) \ не \ является \ вредоносной \ по \ отношению \ к \ v \ и \ j]](/sites/default/files/tex_cache/78d2c2bedd662e4caaca06d1bd26608e.png)
![(\forall j \in \Gamma ') [v(j) \ не \ является \ заразной \ по \ отношению\ к \ v \ и \ j]](/sites/default/files/tex_cache/781521463dbbd28d35e00e8063df649d.png)
![(\forall j \in \Gamma ') [v(j) \ является \ вредоносной \ по \ отношению \ к \ v \ и \ j]](/sites/default/files/tex_cache/5487753f3d9fdfbd58bef59b4203fcc4.png)
![(\forall j \in \Gamma ') [v(j) \ не \ является \ заразной \ по \ отношению \ к \ v \ и \ j]](/sites/default/files/tex_cache/4f7c48433e14ad23dd9c8c1baff44d11.png)
![(\forall j \in \Gamma ') [v(j) \ является \ вредоносной \ по \ отношению \ к \ v \ и \ j]](/sites/default/files/tex_cache/b8f8cb1cd881d3b8fecb9b82b72da538.png)
 - полное множество
- полное множество