НОУ ИНТУИТ | Введение в линейную алгебру. Лекция 7: Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4378 / 711 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

Теги: линейные пространства, метод Гауса, определители, векторы, матрицы

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Примеры решения задач векторной алгебры (см. лекции "Элементы векторной алгебры. Векторы. Координаты векторов. Линейные операции над векторами" и "Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства" )

Пример 1. Даны векторы 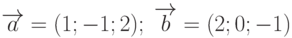$\overrightarrow{a}=(1;-1;2);\;\overrightarrow{b}=(2;0;-1)$ . Найти векторы:

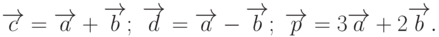
$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b};\;\overrightarrow{d}=\overrightarrow{a}-\overrightarrow{b};\;\overrightarrow{p}=3\overrightarrow{a}+2\overrightarrow{b}.$

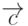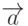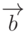Решение. Вектор $\overrightarrow{c}$ представляет из себя сумму двух других векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ , поэтому его координаты могут быть найдены как сумма соответствующих координат суммируемых векторов:

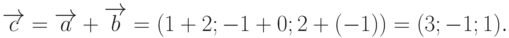
$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}=(1+2;-1+0;2+(-1))=(3;-1;1).$

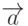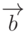Вектор $\overrightarrow{d}$ представляет из себя разность этих же векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ , поэтому его координаты также могут быть найдены очень просто, как разность соответствующих координат вычитаемых векторов:

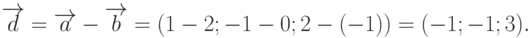
$\overrightarrow{d}=\overrightarrow{a}-\overrightarrow{b}=(1-2;-1-0;2-(-1))=(-1;-1;3).$

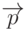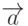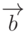Для того чтобы найти третий вектор $\overrightarrow{p}$ , необходимо выполнить промежуточные вычисления, так как на этот раз суммируются не просто векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ , а векторы, предварительно умноженные на 3 и 2, соответственно. Поэтому сначала надо определить координаты векторов $3\overrightarrow{a}$ и $2\overrightarrow{b}$ , а только затем полученные векторы сложить между собой.

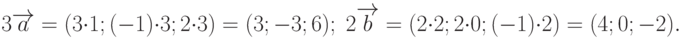
$3\overrightarrow{a}=(3\cdot 1;(-1)\cdot 3;2\cdot 3)=(3;-3;6);\;2\overrightarrow{b}=(2\cdot 2;2\cdot 0;(-1)\cdot 2)=(4;0;-2).$

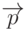Теперь можно вычислить искомый вектор $\overrightarrow{p}$ как

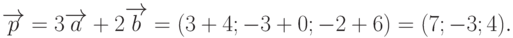
$\overrightarrow{p}=3\overrightarrow{a}+2\overrightarrow{b}=(3+4;-3+0;-2+6)=(7;-3;4).$

Пример 2. Даны проекции силы F на координатные оси как 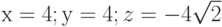$х = 4; у = 4; z = -4\sqrt{2}$ . Найти величину силы F и направление ее действия.

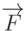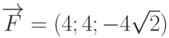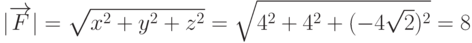Решение. Вектор $\overrightarrow{F}$ имеет координаты (по условию) $\overrightarrow{F}=(4;4;-4\sqrt{2})$ . Так как в задаче речь идет о "величине" силы, то следовательно необходимо определить модуль найденного вектора. Поэтому величина силы находится как $|\overrightarrow{F}|=\sqrt{x^2+y^2+z^2}=\sqrt{4^2+4^2+(-4\sqrt{2})^2}=8$ .

Направление действия силы 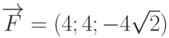$\overrightarrow{F}=(4;4;-4\sqrt{2})$ определяют, используя направляющие косинусы, которые вычисляют по известным формулам:

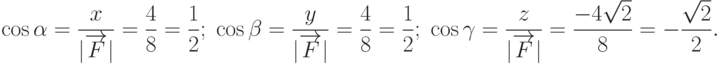
$\cos\alpha=\frac{x}{|\overrightarrow{F}|}=\frac48=\frac12;\;\cos\beta=\frac{y}{|\overrightarrow{F}|}=\frac48=\frac12;\;\cos\gamma=\frac{z}{|\overrightarrow{F}|}=\frac{-4\sqrt{2}}{8}=-\frac{\sqrt{2}}{2}.$

Следовательно сила F, модуль которой равен 8, действует в направлении вектора, образующего с координатными осями углы $\alpha$ =60 $\deg$ ; $\beta$ =60 $\deg$ ; $\gamma$ =135 $\deg$ .

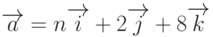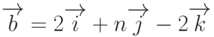Пример 3. Даны векторы $\overrightarrow{a}=n\overrightarrow{i}+2\overrightarrow{j}+8\overrightarrow{k}$ и $\overrightarrow{b}=2\overrightarrow{i}+n\overrightarrow{j}-2\overrightarrow{k}$ . Требуется определить при каком значении n эти векторы будут перпендикулярны?

Решение. Условием перпендикулярности вектором является равенство нулю их скалярного произведения, так как в формулу скалярного произведения входит косинус угла между этими векторами. Известно, что косинус равен нулю, если аргумент его равен $\frac{\pi}{2}$ , т.е. 90 $\deg$ . Поэтому для ответа на вопрос задачи достаточно определить, при каком значении n будет выполняться равенство $\overrightarrow{a}\cdot\overrightarrow{b}=0$ .

По формулам скалярного произведения находим

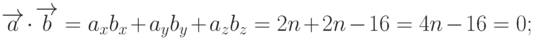
$\overrightarrow{a}\cdot\overrightarrow{b}=a_x b_x+a_y b_y+a_z b_z=2n+2n-16=4n-16=0;$

Из уравнения 4n-16=0 находим, что n=4, т.е. при этом значении n 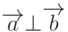$\overrightarrow{a}\bot\overrightarrow{b}$ .

Пример 4. Найти площадь треугольника, заданного вершинами A(1;1;0); B(3;0;-3); C(3;2;4).

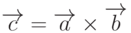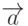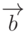Решение. Из геометрической интерпретации векторного произведения двух векторов (рис. 6.2) имеем, что модуль вектора $\overrightarrow{c}=\overrightarrow{a}\times\overrightarrow{b}$ численно равен площади параллелограмма, построенного на векторах $\overrightarrow{a}$ и $\overrightarrow{b}$ , как на сторонах. А из геометрии известно, что диагональ параллелограмма делит последний на два равновеликих треугольника. На основании этого можно выписать формулу для нахождения площади треугольника АВС:

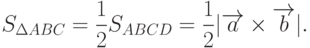
$S_{\Delta ABC}=\frac12 S_{ABCD}=\frac12 |\overrightarrow{a}\times\overrightarrow{b}|.$

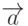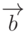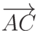Для того, чтобы определить векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ , выберем в качестве вершины любую точку, например А, и найдем векторы $\overrightarrow{AB}$ и $\overrightarrow{AC}$ (т.е. стороны треугольника представляем векторами, при этом выбор направления векторов не будет влиять на результат. Для определенности положим, что начало обоих векторов находится в точке А, тогда конец будет располагаться в точках В и С, соответственно).

Для того чтобы определить координаты вектора $\overrightarrow{AB}$ , вычтем из соответствующих координат "конца" вектора (точка В ) соответствующие координаты "начала" вектора (точка А ). В результате получим

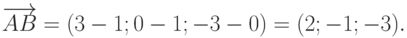
$\overrightarrow{AB}=(3-1;0-1;-3-0)=(2;-1;-3).$

Аналогично находим и координаты вектора 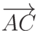$\overrightarrow{AC}$ , с той лишь разницей, что теперь вместо точки В в формуле будем использовать точку С.

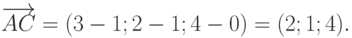
$\overrightarrow{AC}=(3-1;2-1;4-0)=(2;1;4).$

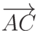Теперь найдем векторное произведение векторов $\overrightarrow{AB}$ и $\overrightarrow{AC}$ по формуле

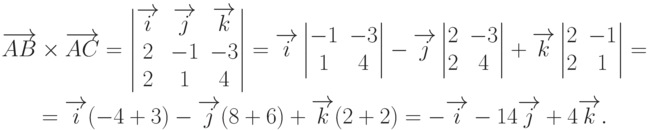
$\begin{gathered} \overrightarrow{AB}\times\overrightarrow{AC}= \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ 2 & -1 & -3 \\ 2 & 1 & 4 \end{vmatrix} =\overrightarrow{i} \begin{vmatrix} -1 & -3 \\ 1 & 4 \end{vmatrix} -\overrightarrow{j} \begin{vmatrix} 2 & -3 \\ 2 & 4 \end{vmatrix} +\overrightarrow{k} \begin{vmatrix} 2 & -1 \\ 2 & 1 \end{vmatrix} = \\ =\overrightarrow{i}(-4+3)-\overrightarrow{j}(8+6)+\overrightarrow{k}(2+2)=-\overrightarrow{i}-14\overrightarrow{j}+4\overrightarrow{k}. \end{gathered}$

Воспользуемся свойством векторного произведения и найдем площадь искомого треугольника.

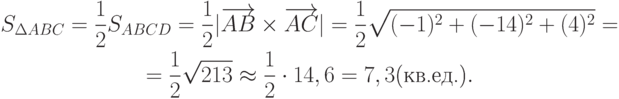
$\begin{gathered} S_{\Delta ABC}=\frac12 S_{ABCD}=\frac12 |\overrightarrow{AB}\times\overrightarrow{AC}|=\frac12\sqrt{(-1)^2+(-14)^2+(4)^2}= \\ =\frac12\sqrt{213}\approx\frac12\cdot 14,6 = 7,3 \text{(кв.ед.)}. \end{gathered}$

Пример 5. Вычислить объем тетраэдра, вершины которого находятся в точках A(1;1;2); B(2;3;-1); C(2;-2;4); D(-1;1;3)

Решение. Из геометрической интерпретации смешанного произведения трех векторов (рис. 6.3) известно, что результат равен объему параллелепипеда, построенного на трех перемножаемых векторах как на сторонах. При этом, если векторы образуют правую тройку, то объем выражается положительным числом, а , если векторы образуют левую тройку, то отрицательным. Кроме того, из аналитической геометрии известно, что любой параллелепипед можно разделить на шесть одинаковых тетраэдров. Следовательно, основываясь на свойстве смешанного произведения трех векторов, можно записать:

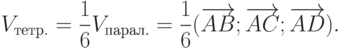
$V_{\tetx{тетр.}}=\frac16 V_{\text{парал.}}=\frac16(\overrightarrow{AB};\overrightarrow{AC};\overrightarrow{AD}).$

Определим векторы $\overrightarrow{AB}, \overrightarrow{AC}$ и $\overrightarrow{AD}$ . Для этого, как и в предыдущем примере, будем считать, без ограничения общности, точку А "началом" каждого из векторов, а точки В, С и D - "концами" этих векторов. Тогда вычитая координаты "начала" из координат "конца" получаем искомые векторы.

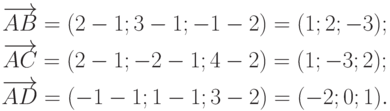
$\begin{gathered} \overrightarrow{AB}=(2-1;3-1;-1-2)=(1;2;-3); \\ \overrightarrow{AC}=(2-1;-2-1;4-2)=(1;-3;2); \\ \overrightarrow{AD}=(-1-1;1-1;3-2)=(-2;0;1). \end{gathered}$

После того как необходимые для вычислений векторы найдены, несложно, пользуясь расчетной формулой смешанного произведения векторов, найти объем тетраэдра.

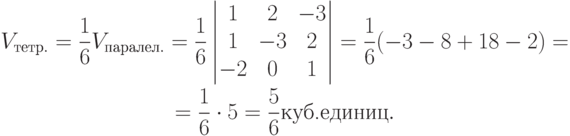
$\begin{gathered} V_{\text{тетр.}}=\frac16 V_{\text{паралел.}}=\frac16 \begin{vmatrix} 1 & 2 & -3 \\ 1 & -3 & 2 \\ -2 & 0 & 1 \end{vmatrix} =\frac16(-3-8+18-2)= \\ =\frac16\cdot 5=\frac56\text{куб.единиц}. \end{gathered}$

Замечание. Если объем тетраэдра (или параллелепипеда) получился отрицательным, то это значит, что выбрана левая тройка векторов. Для исправления ориентации тройки векторов (и знака результата) достаточно переставить две строки в определителе (см. "Определители и их свойства. Определители второго порядка и их свойства. Определители третьего порядка и их свойства. Миноры и алгебраические дополнения" , свойство 2).

Дальше >>

Авторизоваться

Введение в линейную алгебру

Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства

Вопросы и ответы