|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование логарифмических и экспоненциальных функций. Решение дифференциального уравнения Риша
Вычисление рациональной и логарифмической части интеграла
Интегрируя правильную рациональную функцию 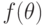 от
от  , поступаем так же,
как и в случае интегрирования правильных рациональных функций от независимой
переменной
, поступаем так же,
как и в случае интегрирования правильных рациональных функций от независимой
переменной  .
.
Прежде всего разлагаем знаменатель
подынтегральной функции на неприводимые множители, добавляя, если необходимо,
к полю констант  новые алгебраические над
новые алгебраические над  константы. Можно предполагать,
что эти константы уже принадлежат полю
константы. Можно предполагать,
что эти константы уже принадлежат полю  .
(Отметим, что, в отличие от случая поля рациональных функций,
даже после добавления новых констант знаменатель не обязан разлагаться
на линейные множители.) Далее выполняем разложение подынтегральной
функции в сумму простейших дробей.
.
(Отметим, что, в отличие от случая поля рациональных функций,
даже после добавления новых констант знаменатель не обязан разлагаться
на линейные множители.) Далее выполняем разложение подынтегральной
функции в сумму простейших дробей.
Пусть 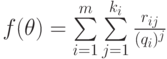 - разложение
в сумму простейших дробей
- разложение
в сумму простейших дробей ![r_{ij}, q_i\in \EuScript F_{n-1}[\theta]](/sites/default/files/tex_cache/c2fdb64247b7675d851597831fdfe497.png) .
Без потери общности можно предполагать, что старшие коэффициенты полиномов
.
Без потери общности можно предполагать, что старшие коэффициенты полиномов  равны 1 (поскольку
равны 1 (поскольку  - поле). Из условия, что
- поле). Из условия, что 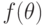 - правильная
рациональная функция, следует неравенство
- правильная
рациональная функция, следует неравенство  для любых
для любых  и
и  . Как и для рациональных функций от
. Как и для рациональных функций от  показывается, что рациональная
часть интеграла может содержать в знаменателе только функции
показывается, что рациональная
часть интеграла может содержать в знаменателе только функции  в степенях
не выше
в степенях
не выше  . (При дифференцировании простейшей дроби
. (При дифференцировании простейшей дроби 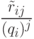 получается слагаемое
получается слагаемое 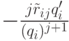 ,
которое может сократиться
только со слагаемыми, полученными от дифференцирования других простейших
дробей, или со слагаемыми, полученными от разложения в сумму простейших дробей
подынтегральной
функции.) Из этого замечания следует также, что можно отдельно интегрировать
слагаемые, относящиеся к разным полиномам
,
которое может сократиться
только со слагаемыми, полученными от дифференцирования других простейших
дробей, или со слагаемыми, полученными от разложения в сумму простейших дробей
подынтегральной
функции.) Из этого замечания следует также, что можно отдельно интегрировать
слагаемые, относящиеся к разным полиномам  , т. е. вычислять
интегралы
, т. е. вычислять
интегралы 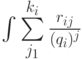 для каждого
для каждого  отдельно.
Если
отдельно.
Если  , то будем искать интеграл в виде
, то будем искать интеграл в виде ![\smash[t]{\frac
{\tilde r_{ik_i-1}}{(q_i)^{k_i-1}}}
+ \tilde g](/sites/default/files/tex_cache/f5c9ea319c77d23bd620ba8b91b68395.png) , где
, где 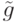 - интеграл от некоторой
правильной дроби
со знаменателем
- интеграл от некоторой
правильной дроби
со знаменателем 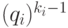 . Для нахождения полинома
. Для нахождения полинома  нужно в множестве полиномов, степень которых меньше
нужно в множестве полиномов, степень которых меньше  ,
найти решение сравнения
,
найти решение сравнения 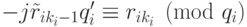 .
Это можно сделать, например, при помощи расширенного алгоритма Евклида,
поскольку
из неприводимости полинома
.
Это можно сделать, например, при помощи расширенного алгоритма Евклида,
поскольку
из неприводимости полинома  следует, что он взаимно прост с
полиномом
следует, что он взаимно прост с
полиномом 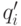 , степень которого на 1 меньше степени
, степень которого на 1 меньше степени  .
(Следует помнить, что
дифференцирование осуществляется по независимой переменной
.
(Следует помнить, что
дифференцирование осуществляется по независимой переменной  , т. е.
дифференцируются
не только
, т. е.
дифференцируются
не только  , но и коэффициенты, и
, но и коэффициенты, и 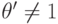 ).
После нескольких шагов описанного типа (в которых нет неразрешимых шагов)
мы придем к случаю, когда
).
После нескольких шагов описанного типа (в которых нет неразрешимых шагов)
мы придем к случаю, когда  .
Обработка этого случая заключается в проверке того, что частное от деления
числителя
на производную по
.
Обработка этого случая заключается в проверке того, что частное от деления
числителя
на производную по  от знаменателя является константой. Если это
не так, то исходная функция неинтегрируема в элементарном виде.
от знаменателя является константой. Если это
не так, то исходная функция неинтегрируема в элементарном виде.
Так же, как и при интегрировании рациональных функций с постоянными коэффициентами, мы можем при нахождении рациональной части интеграла воспользоваться разложением знаменателя на свободные от квадратов множители, определить знаменатель рациональной части интеграла (кратность любого неприводимого множителя снова на 1 меньше его кратности в знаменателе подынтегрального выражения) и искать \vad числитель методом неопределенных коэффициентов. Для нахождения логарифмической части может потребоваться разложить знаменатель (свободный от квадратов) на неприводимые множители.
Интегрирование экспоненциальных функций
Интегрирование экспоненциальных функций проходит во многом параллельно интегрированию логарифмических функций, хотя есть существенные отличия. Мы работаем в следующих предположениях.
Дано конструктивное поле констант  ,
,  - независимая переменная над этим полем,
- независимая переменная над этим полем, 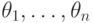 - последовательность регулярных
мономов,
- последовательность регулярных
мономов, 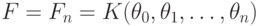 -
соответствующее поле элементарных функций,
-
соответствующее поле элементарных функций,  . Предполагается, что
. Предполагается, что 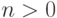 ,
,  - экспонента над
- экспонента над 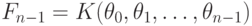 и что мы
умеем интегрировать функции из поля
и что мы
умеем интегрировать функции из поля 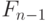 .
.
Описание алгоритма, позволяющего найти неопределенный интеграл функции  , если
он является элементарной функцией,
начнем снова с леммы о разложении. Ее формулировка будет слегка
отличаться от логарифмического случая. Связано это с тем, что в
экспоненциальном
случае
, если
он является элементарной функцией,
начнем снова с леммы о разложении. Ее формулировка будет слегка
отличаться от логарифмического случая. Связано это с тем, что в
экспоненциальном
случае 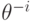 ведет себя как полином: при дифференцировании
ее степень не меняется.
Поэтому в разложении функции в сумму простейших дробей слагаемые со
знаменателем
ведет себя как полином: при дифференцировании
ее степень не меняется.
Поэтому в разложении функции в сумму простейших дробей слагаемые со
знаменателем 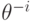 , где
, где  - натуральное число, мы будем
относить к полиномиальной
части и называть соответствующую сумму
- натуральное число, мы будем
относить к полиномиальной
части и называть соответствующую сумму ![\smash[b]{\sum\limits_{i=-m}^k}
a_i\theta ^i](/sites/default/files/tex_cache/c97c3e94e7864f89c6def20915f54bf8.png) обобщенным полиномом.
обобщенным полиномом.
Пусть ![f(\theta )=p(\theta )+\smash[t]{\frac {r(\theta )}{q(\theta
)}}](/sites/default/files/tex_cache/8756935f5671fa92c36ed0a675e8c2b0.png) - разложение функции
- разложение функции  в сумму
обобщенного полинома
и правильной рациональной функции, знаменатель которой не делится на
в сумму
обобщенного полинома
и правильной рациональной функции, знаменатель которой не делится на  (как рациональной функции от
(как рациональной функции от  с коэффициентами
из поля
с коэффициентами
из поля 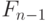 ). Покажем, что можно отдельно рассматривать
задачу
для полиномиальной части
). Покажем, что можно отдельно рассматривать
задачу
для полиномиальной части  и правильной рациональной
части
и правильной рациональной
части 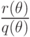 .
.
26.1. ЛЕММА (о разложении).
Элементарный интеграл функции 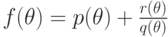 существует тогда и только тогда, когда существуют элементарные интегралы
функций
существует тогда и только тогда, когда существуют элементарные интегралы
функций  и
и ![\smash[t]{\frac {r(\theta )}{q(\theta
)}}](/sites/default/files/tex_cache/dc148847b61a52b6a85f636593b54327.png) .
.
ДОКАЗАТЕЛЬСТВО.
Согласно теореме Лиувилля, если элементарный интеграл
существует, то он имеет вид ![g=v_0+\smash[b]{\sum\limits_{i=1}^m} c_i\log
v_i](/sites/default/files/tex_cache/4c99b7ad9b22474eb31052dd7a07202b.png) , т. е.
функцию
, т. е.
функцию  можно представить в виде
можно представить в виде
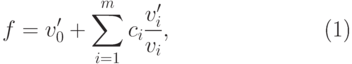 |
( 26.1) |
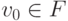 ,
, 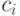 - алгебраические над
- алгебраические над  константы,
константы,  - элементы
из дифференциального поля, получающегося присоединением к
- элементы
из дифференциального поля, получающегося присоединением к 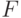 конечного числа
алгебраических над
конечного числа
алгебраических над  констант. Дифференцирование
констант. Дифференцирование  обозначает дифференцирование по
обозначает дифференцирование по  .
Разложим
.
Разложим 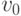 в сумму обобщенного полинома
в сумму обобщенного полинома 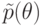 от
от  и правильной рациональной функции
и правильной рациональной функции  от
от  (знаменатель которой не делится на
(знаменатель которой не делится на  ).
Заметим, что степень (по
).
Заметим, что степень (по  ) полинома
) полинома 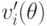 на этот раз равна степени
(по
на этот раз равна степени
(по  ) полинома
) полинома 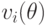 (используется то,
что
(используется то,
что 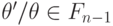 ), поэтому слагаемые вида
), поэтому слагаемые вида 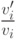 , где
, где  -
полиномы от
-
полиномы от  не являются правильными рациональными
функциями.
Предполагая, что
не являются правильными рациональными
функциями.
Предполагая, что  и
старшие коэффициенты полиномов
и
старшие коэффициенты полиномов  равны 1, мы находим, что старший коэффициент полинома
равны 1, мы находим, что старший коэффициент полинома 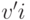 равен
равен 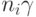 , т. е.
, т. е. 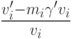 -
правильная рациональная от
-
правильная рациональная от  функция, интегрируемая в элементарном виде тогда и только тогда, когда
интегрируема
функция
функция, интегрируемая в элементарном виде тогда и только тогда, когда
интегрируема
функция 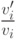 .
.Интегрирование обобщенной полиномиальной части
Решая уравнение 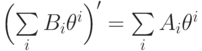 методом неопределенных
коэффициентов,
мы приходим к системе дифференциальных уравнений
методом неопределенных
коэффициентов,
мы приходим к системе дифференциальных уравнений 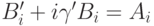 , называемых
уравнениями Риша, для которых требуется найти решения в поле
, называемых
уравнениями Риша, для которых требуется найти решения в поле 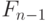 .
.
Вычисление рациональной и логарифмической части интеграла
В основном, вычисления проходят параллельно случаю, когда  является
логарифмом. Основные отличия обусловлены тем, что при дифференцировании по
является
логарифмом. Основные отличия обусловлены тем, что при дифференцировании по  полинома от
полинома от  со старшим коэффициентом 1
степень полинома не меняется.
Поэтому чуть сложнее обосновать взаимную простоту неприводимого полинома
со старшим коэффициентом 1
степень полинома не меняется.
Поэтому чуть сложнее обосновать взаимную простоту неприводимого полинома  и его производной
и его производной 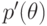 .
.
26.2. ЛЕММА.
Пусть  - дифференциальное поле,
- дифференциальное поле,  -
экспонента
над
-
экспонента
над  ,
, 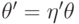 ,
, 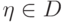 ,
, ![p(\theta)\in D[\theta]](/sites/default/files/tex_cache/982ba7c19ad30f36757f5cdffa3373e2.png) -
неприводимый полином со старшим коэффициентом равным 1. Если
-
неприводимый полином со старшим коэффициентом равным 1. Если 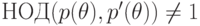 , то
, то  .
.
ДОКАЗАТЕЛЬСТВО.
Пусть  . Тогда
. Тогда
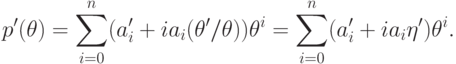
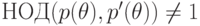 ,
то
,
то 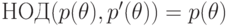 в силу неприводимости
в силу неприводимости  ,
т. е.
,
т. е. 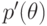 отличается от
отличается от  множителем
из поля
множителем
из поля  . Значит
отношение
. Значит
отношение  для всех ненулевых
коэффициентов не
зависит от
для всех ненулевых
коэффициентов не
зависит от  . Предположим, что
. Предположим, что 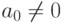 . Тогда
. Тогда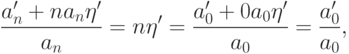
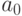 удовлетворяет условию
удовлетворяет условию 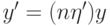 . Этому же
условию удовлетворяет
элемент
. Этому же
условию удовлетворяет
элемент 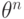 . Поскольку любые два решения линейного
однородного
дифференциального уравнения первого порядка отличаются постоянным множителем,
получаем
. Поскольку любые два решения линейного
однородного
дифференциального уравнения первого порядка отличаются постоянным множителем,
получаем  для некоторой константы
для некоторой константы  , что противоречит
трансцендентности
, что противоречит
трансцендентности  . Доказательство леммы закончено.
. Доказательство леммы закончено.Учитывая лемму и то, что дроби со знаменателями 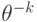 относятся к
обобщенной полиномиальной части, можно почти дословно повторить рассуждения о
понижении степени знаменателя при интегрировании простейших дробей, приведенные
выше для логарифмического случая. Небольшое отличие состоит в том, что при этих
вычислениях мы выходим за рамки работы с правильными дробями, и у нас
появляются
полиномиальные слагаемые нулевой степени относительно
относятся к
обобщенной полиномиальной части, можно почти дословно повторить рассуждения о
понижении степени знаменателя при интегрировании простейших дробей, приведенные
выше для логарифмического случая. Небольшое отличие состоит в том, что при этих
вычислениях мы выходим за рамки работы с правильными дробями, и у нас
появляются
полиномиальные слагаемые нулевой степени относительно  .
Эти слагаемые мы
можем обрабатывать при интегрировании обобщенной полиномиальной части, если
интегрирование рациональной части выполнено до интегрирования обобщенного
полинома.
.
Эти слагаемые мы
можем обрабатывать при интегрировании обобщенной полиномиальной части, если
интегрирование рациональной части выполнено до интегрирования обобщенного
полинома.
В заключение перечислим основные шаги алгоритма интегрирования трансцендентных функций.
- Выделить в подынтегральном выражении
последовательность подвыражений,
порождаемое которыми дифференциальное поле содержит подынтегральное
выражение.
С помощью структурной теоремы проверить, является ли выписанная
последовательность
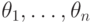 последовательностью
регулярных
мономов. При положительном ответе переходить к следующему пункту, в противном
случае попытаться найти другую систему образующих. Если после нескольких
попыток "хорошую" систему образующих найти не удается, нужно
использовать
методы интегрирования, позволяющие работать с алгебраическими расширениями (в
данной книге не описанные).
последовательностью
регулярных
мономов. При положительном ответе переходить к следующему пункту, в противном
случае попытаться найти другую систему образующих. Если после нескольких
попыток "хорошую" систему образующих найти не удается, нужно
использовать
методы интегрирования, позволяющие работать с алгебраическими расширениями (в
данной книге не описанные). - Представить подынтегральное выражение в виде рациональной функции
переменной
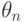 с коэффициентами из дифференциального поля
с коэффициентами из дифференциального поля 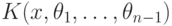 . Если
. Если 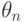 - логарифм, то
разложить подынтегральное
выражение в суммы полинома от
- логарифм, то
разложить подынтегральное
выражение в суммы полинома от 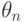 и правильной
рациональной дроби.
Если
и правильной
рациональной дроби.
Если 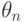 - экспонента, то разложить подынтегральное
выражение в сумму
обобщенного полинома и правильной рациональной дроби, знаменатель которой
не
делится на
- экспонента, то разложить подынтегральное
выражение в сумму
обобщенного полинома и правильной рациональной дроби, знаменатель которой
не
делится на 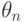 .
. - Найти рациональную часть интеграла. При этом нет необходимости разлагать знаменатель подынтегрального выражения на неприводимые множители, достаточно выполнить только разложение на свободные от квадратов множители.
- Применить алгоритм вычисления логарифмической части интеграла. Здесь может потребоваться разложить знаменатель на неприводимые множители. Если логарифмическая часть найдена, то перейти к следующему шагу. Если алгоритм вычисления логарифмической части приводит к несовместным уравнениям, то исходное выражение неинтегрируемо в элементарных функциях, сообщением о чем и следует закончить работу в этом случае.
- Интегрировать полиномиальную (обобщенную полиномиальную)
часть
подынтегрального выражения (без свободного члена). Находится ограничение на
степень решения, далее решение находится методом неопределенных
коэффициентов.
Получается система линейных дифференциальных уравнений первого порядка, для
которой нужно найти решения в поле
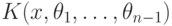 . Если
какое-либо из получившихся уравнений не имеет решений в дифференциальном
поле
. Если
какое-либо из получившихся уравнений не имеет решений в дифференциальном
поле 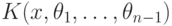 , то исходная функция неинтегрируема в классе
элементарных
функций.
, то исходная функция неинтегрируема в классе
элементарных
функций. - Интегрировать свободный член, представляющий собой элемент из поля
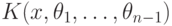 . Если
. Если 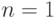 ,
то получается задача
интегрирования рациональной функции с постоянными коэффициентами, если
,
то получается задача
интегрирования рациональной функции с постоянными коэффициентами, если 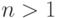 ,
то имеем задачу аналогичную исходной, но число образующих дифференциального
поля уменьшилось на 1. Выполняем все те же шаги алгоритма, начиная с шага
2.
,
то имеем задачу аналогичную исходной, но число образующих дифференциального
поля уменьшилось на 1. Выполняем все те же шаги алгоритма, начиная с шага
2.
