|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Редуцированные базисы решетки. Редуцирование базиса в решетке
Реализация полученных формул описывается следующим алгоритмом:
А36. АЛГОРИТМ (переставить-  -ый-элемент-базиса-
-ый-элемент-базиса-  -
-  -
-  -м).
-м).
![\begin{equation*}
\text{Дано:\quad $k\in\mathbb Z $, } \\
\text{\qquad $L$ - решетка, } \\
\text{\qquad $\mu$ - нижняя треугольная матрица коэффициентов, вычисляемых
по формулам (19.1) и (19.2),} } \\
\text{\qquad $B$ - вектор элементов типа вещественное число с индексом $1..n$. }\\
\text{Элементы вектора $B$ - это квадраты длин соответствующих векторов из} \\
\text{ортогонального базиса $b1$, вычисляемого по формулам
(19.1) и (19.2).} \\
\text{Надо:\qquad $L, \mu , B$ } \\
\text{\qquad В векторе $L$.базис поменялись местами два элемента. } \\
\text{ \qquad Соответствующие изменения
произошли с элементами матрицы $\mu$ и вектора $B$.} } \\
\text{Обозначения:\quad $n == L$.ранг } \\
\text{\qquad $b == L$.базис }\\
\text{Переменные:\quad \qquad $BB, \mu\mu$ - вещественные числа } \\
\text{Начало} \\
\text{$\mu \mu := \mu [k,k-1]$ } \\
\text{$BB := B[k] + \mu\mu^2 \cdot B[k-1]$} \\
\text{$\mu [k,k-1] :=\dfrac{\mu\mu \cdot B[k-1]}{BB}$} \\
\text{$B[k] :=\dfrac{B[k-1]\cdot B[k]}{BB}$ } \\
\text{$B[k-1] := BB$ } \\
\text{$\begin{pmatrix}
b[k-1] \\ b[k]\end{pmatrix} := \begin{pmatrix}
b[k] \\ b[k-1]\end{pmatrix}$ } \\
\text{цикл для $i$ от $1$ до $k-2$ } \\
\text{\qquad $\begin{pmatrix}
\mu [k-1,i] \\ \mu [k,i] \end{pmatrix} := \begin{pmatrix}
\mu [k,i] \\ \mu [k-1,i] \end{pmatrix}$ } \\
\text{конец цикла } \\
\text{цикл для $i$ от $k+1$ до $n$ } \\
\text{\qquad $\begin{pmatrix}
\mu [i,k-1] \\ \mu [i,k] \end{pmatrix} := \begin{pmatrix}
1 & \mu [k,k-1] \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1
\\ 1 & -\mu\mu \end{pmatrix}
$
}
\text{$\begin{pmatrix} \mu [i,k-1] \\ \mu [i,k] \end{pmatrix}$ } \\
\text{конец цикла} \\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/6bba1e8b4a18eedba291f4eaefbc4117.png)
Переходим к обоснованию алгоритма A33 построения редуцированного базиса решетки. Оно состоит из доказательства двух утверждений. Во-первых, докажем, что если алгоритм завершит свою работу, то в результате получим редуцированный базис данной решетки. Во-вторых, докажем, что для любого исходного базиса решетки алгоритм после конечного числа шагов закончит работу.
Для доказательства первого утверждения заметим, что мы выполняем над
элементами базиса только элементарные преобразования, которые переводят базис 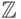 -модуля в другой базис того же самого
-модуля в другой базис того же самого 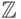 -модуля,
т. к. и перестановка
элементов базиса и прибавление к одному из элементов целого кратного другого
-
обратимые операции. Таким образом, в любой момент времени
-модуля,
т. к. и перестановка
элементов базиса и прибавление к одному из элементов целого кратного другого
-
обратимые операции. Таким образом, в любой момент времени  представляет
собой базис исходной решетки. Элементы этого базиса с 1-го по
представляет
собой базис исходной решетки. Элементы этого базиса с 1-го по  -ый
представляют собой редуцированный базис подрешетки, порожденной этими
элементами, т. к. для них выполнены условия (19.4) и (19.5).
Когда мы производим
преобразования вектора
-ый
представляют собой редуцированный базис подрешетки, порожденной этими
элементами, т. к. для них выполнены условия (19.4) и (19.5).
Когда мы производим
преобразования вектора ![b[k]](/sites/default/files/tex_cache/268ae3e03e375138a69be5df3057b7d1.png) , направленные на то, чтобы для него
выполнялись
условия (19.4), эти преобразования никак не отражаются на векторах с
1-го по
, направленные на то, чтобы для него
выполнялись
условия (19.4), эти преобразования никак не отражаются на векторах с
1-го по  -ый, а если мы производим перестановку
-ый, а если мы производим перестановку  -го элемента базиса с
-го элемента базиса с  -ым, то уменьшаем длину редуцированной части базиса
на 1 (если она
больше 1; меньше 1 длина редуцированной части базиса быть не может) и
одновременно уменьшаем значение
-ым, то уменьшаем длину редуцированной части базиса
на 1 (если она
больше 1; меньше 1 длина редуцированной части базиса быть не может) и
одновременно уменьшаем значение  . Для векторов с 1-го по
. Для векторов с 1-го по  -ый снова
выполнены условия (19.4) и (19.5). Таким образом, если алгоритм
завершил свою
работу, то получившийся базис - редуцированный базис исходной решетки
-ый снова
выполнены условия (19.4) и (19.5). Таким образом, если алгоритм
завершил свою
работу, то получившийся базис - редуцированный базис исходной решетки  .
.
Прежде чем перейти к доказательству второго утверждения, приведем несколько определений и задач различной степени сложности.
20.1. УПРАЖНЕНИЕ.
Пусть 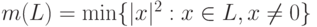 . Показать,
что для любой решетки
. Показать,
что для любой решетки  выполняется неравенство
выполняется неравенство 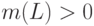 .
.
Введем обозначение
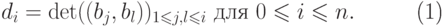 |
( 20.12) |
20.2. УПРАЖНЕНИЕ. Показать, что для всех  от 1 до
от 1 до  выполняется равенство
выполняется равенство 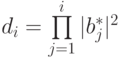 .
.
Для всех  числа
числа 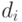 могут быть
интерпретированы как квадраты
детерминантов решеток ранга
могут быть
интерпретированы как квадраты
детерминантов решеток ранга  , порожденных векторами
, порожденных векторами  в
векторных пространствах
в
векторных пространствах 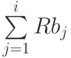 .
.
20.3. УПРАЖНЕНИЕ. Показать, что каждая такая решетка содержит
ненулевой вектор  ,
удовлетворяющий неравенству
,
удовлетворяющий неравенству
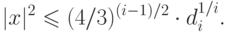
Переходим теперь к доказательству второй части утверждения о корректности алгоритма построения редуцированного базиса. Пусть
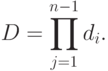
Из упражнения 20.2 следует, что
значение  меняется только тогда, когда
изменяется хотя бы один из векторов
меняется только тогда, когда
изменяется хотя бы один из векторов 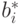 . Это может произойти
только при
перестановке двух векторов базиса. При этом новое значение
. Это может произойти
только при
перестановке двух векторов базиса. При этом новое значение 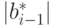 равно
равно 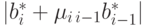 , что по условию
меньше, чем 3/4
от прежнего значения этой величины. Таким образом, при каждой выполняемой
перестановке элементов базиса значение величины
, что по условию
меньше, чем 3/4
от прежнего значения этой величины. Таким образом, при каждой выполняемой
перестановке элементов базиса значение величины  умножается на
положительное число, меньшее 3/4. Из упражнений 20.1-20.3 следует, что
умножается на
положительное число, меньшее 3/4. Из упражнений 20.1-20.3 следует, что  ограничено снизу некоторой положительной величиной, следовательно,
перестановка элементов выполняется в алгоритме только конечное число раз,
обозначим его
ограничено снизу некоторой положительной величиной, следовательно,
перестановка элементов выполняется в алгоритме только конечное число раз,
обозначим его  . При каждом выполнении перестановки значение
. При каждом выполнении перестановки значение  уменьшается
на 1, при выполнении команд, следующих за ключевым словом "иначе" в
алгоритме,
значение
уменьшается
на 1, при выполнении команд, следующих за ключевым словом "иначе" в
алгоритме,
значение  увеличивается на 1. Начальное значение
увеличивается на 1. Начальное значение  равно 2, алгоритм
продолжает работу до тех пор, пока
равно 2, алгоритм
продолжает работу до тех пор, пока  , следовательно,
ситуация "иначе"
встречается
, следовательно,
ситуация "иначе"
встречается 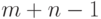 раз, т.е. тело цикла "пока" выполняется
конечное число
раз. Таким образом, алгоритм завершает работу после выполнения конечного числа
шагов. Ниже мы оценим это число для случая, когда все координаты исходного
базиса решетки - целые числа.
раз, т.е. тело цикла "пока" выполняется
конечное число
раз. Таким образом, алгоритм завершает работу после выполнения конечного числа
шагов. Ниже мы оценим это число для случая, когда все координаты исходного
базиса решетки - целые числа.
Итак, переходим к оценке сложности алгоритма построения редуцированного базиса решетки в предположении, что все координаты исходного базиса являются целыми числами. Именно такой случай нам понадобится для получения алгоритма факторизации полиномиальной сложности. Наша цель сейчас - доказательство следующего предложения.
