Введение

Алгоритмы компьютерной алгебры. Компьютерная алгебра имеет дело с алгоритмами, которые существенно отличаются от алгоритмов, используемых в вычислительной математике. Алгоритмы вычислительной математики должны давать возможность решать задачу с требуемой точностью при заданных вычислительных ресурсах, наиболее существенными из которых являются ограничения по используемой памяти и времени счета. В компьютерной алгебре вычисления обычно производятся без округления, анализу сходимости уделяется значительно меньше внимания, но используется значительно более широкий набор математических, в первую очередь алгебраических, объектов сложной структуры, и ограничения по времени счета, а особенно по используемой памяти, становятся гораздо более обременительными.

Применение компьютеров в алгебраических исследованиях поставило перед специалистами ряд новых задач и в то же время заставило заново пересмотреть задачи, считавшиеся решенными полностью и окончательно. В частности, к ним относились задачи, для которых был предложен метод, позволяющий решать их "за конечное число шагов" . При этом методы решения конкретных задач обычно отличались большим разнообразием, и универсальные методы для конкретных вычислений практически не использовались. С применением компьютеров для алгебраических вычислений потребовалось реализовать универсальные алгоритмы в виде программ для ЭВМ, и оказалось, что они позволяют решать только очень небольшие задачи. С увеличением размера задачи резко возрастало время счета и необходимая память компьютера. Это сделало актуальным поиск более эффективных алгоритмов решения алгебраических задач.

В конце прошлого века бурно развивались исследования в трех областях компьютерной алгебры — теории базисов Гребнера, факторизации многочленов и интегрирования в конечном виде. Именно этим вопросам, в первую очередь, посвящено настоящее пособие.

Оно начинается с рассмотрения проблемы представления данных, которую можно сформулировать в следующем виде. Имеется множество объектов T и на нем отношение эквивалентности 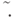Требуется в каждом классе эквивалентных объектов выбрать единственного представителя этого класса, для основных алгебраических областей: кольца целых чисел, поля рациональных чисел, конечных полей, кольца многочленов и поля рациональных функций, алгебраических и трансцендентных расширений полей. Кроме того, в "Введение" рассматриваются арифметические операции в этих областях.

Отдельная лекция ( "Проблема представления данных" ) посвящена алгоритмам вычисления наибольших общих делителей целых чисел и многочленов. Здесь же приводятся некоторые оценки для коэффициентов делителя многочлена от одной переменной.

Задача представления данных для факторколец кольца многочленов приводит к введению понятия базисов Гребнера полиномиальных идеалов. Рассматривая образующие полиномиального идеала как систему нелинейных алгебраических уравнений, базис Гребнера можно трактовать как некоторую каноническую форму этой системы. Для случая многочленов от одной переменной над некоторым полем в качестве такой "канонической формы" можно рассматривать наибольший общий делитель этих многочленов, который может быть получен, например, с помощью алгоритма Евклида. Для системы линейных уравнений от многих переменных в качестве "канонической формы" можно взять диагональную форму системы (т. е. систему вида 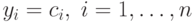), которая может быть получена с помощью метода Гаусса. В общем случае алгоритмы построения базиса Гребнера можно считать обобщением алгоритма Евклида и метода Гаусса.

Теория базисов Гребнера рассматривается в "Наибольший общий делитель и последовательности полиномиальных остатков" . Изложение не ограничивается случаем полиномиальных идеалов: строится более общая теория, применимая также к подмодулям свободных полиномиальных, дифференциальных и разностных модулей. Наряду с классическими базисами Гребнера рассматривается их специальный случай, называемый инволютивными базисами.

Базисы Гребнера имеют многочисленные приложения. В частности, они позволяют определить, совместна ли система нелинейных алгебраических уравнений, и, если система совместна, то определить, сколько эта система имеет решений над алгебраически замкнутым полем (если множество решений бесконечно, то определить размерность многообразия решений). Эти вопросы изучаются в рамках теории размерностных многочленов (многочленов Гильберта). Свойства таких многочленов и алгоритмы их вычисления приведены в "Базисы Гребнера" .

"Целозначные многочлены и размерностные многочлены матриц и подмножеств в Nm" посвящена задаче разложения многочленов на неприводимые множители. Мы рассматриваем эту задачу в следующей постановке: дан многочлен с целыми коэффициентами от одной переменной, требуется разложить его на неприводимые множители. С точки зрения "чистого" математика эта задача давно решена полностью и окончательно: получен алгоритм, позволяющий находить требуемое разложение "за конечное число шагов". Один из таких алгоритмов получен в 1882 году Кронекером, чьим именем он и называется в настоящее время, хотя за 100 лет до Кронекера этот алгоритм был известен австрийскому астроному Шуберту. Следующий шаг в исследовании алгоритмов факторизации был сделан только в 60-х годах прошлого столетия, когда был найден достаточно эффективный алгоритм для разложения на множители многочленов с коэффициентами из конечного поля. Использование этого алгоритма в сочетании с леммой Гензеля позволило получить алгоритмы факторизации многочленов с целыми коэффициентами, пригодные для практической реализации. С конца 60-х годов прошлого века появляется большое количество работ по факторизации. Предлагаются усовершенствования алгоритмов, направленные на увеличение их быстродействия, на расширение области их применения, в частности, рассматривается задача факторизации многочленов от одной и многих переменных с коэффициентами из конечных полей, из полей алгебраических чисел и т.д. Крупным вкладом в теорию факторизации многочленов явилась работа [ 24 ] , позволившая получить алгоритм факторизации, сложность которого оценивается полиномом от степени исходного многочлена.

Наконец, "Алгоритмы вычисления размерностных многочленов" посвящена одной из проблем дифференциальной компьютерной алгебры.

Дифференциальные кольца и поля, в которых наряду с арифметическими операциями имеется одна или несколько операций дифференцирования, - это активно исследуемые объекты компьютерной алгебры. Важным частным случаем дифференциальных полей являются поля элементарных функций, получающиеся из поля рациональных функций от одной переменной последовательным присоединением алгебраических элементов, экспонент и логарифмов (таким образом формализуется основная масса формул, с которыми мы привыкли иметь дело в курсе анализа). Алгебраические зависимости, которые могут существовать между образующими таких расширений, описывает так называемая структурная теорема. (В общем случае дифференциальные поля имеют очень сложную структуру и проблема представления данных для них алгоритмически неразрешима.)

Операция дифференцирования легко описывается алгебраически, и ее реализация не представляет трудностей. Гораздо сложнее обстоит дело с обратной операцией - интегрированием. Если F - дифференциальное поле и 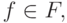то не обязательно существует 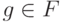такой, что g'=f. Задача интегрирования в конечном виде в общем случае формулируется следующим образом. Пусть и - два класса дифференциальных полей. Требуется построить алгоритм, который для любого элемента f любого дифференциального поля F из класса либо находит дифференциальное поле G в классе и элемент такой, что g'=f, либо доказывает, что такого элемента не существует ни в каком поле класса 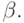В классической постановке задачи - класс полей элементарных функций. Различные методы интегрирования изучаются в курсе математического анализа, но до недавнего времени они не были оформлены в виде алгоритмов, применимых к широкому классу функций, в частности, эти методы часто позволяли проинтегрировать функцию, если элементарный интеграл у нее существует, но далеко не всегда позволяли доказать отсутствие элементарного интеграла.

Алгоритм интегрирования в конечном виде функций из чисто трансцендентного расширения поля рациональных функций, порожденного экспонентами и логарифмами, был сформулирован в 1969 году Ришем [ 29 ] . Проверка, принадлежит ли подынтегральная функция данному классу, осуществляется с помощью структурной теоремы. Далее теорема Лиувилля позволяет определить вид элементарного интеграла, если такой существует. Вычисление интеграла или доказательство его отсутствия производится методом неопределенных коэффициентов с использованием рекурсии. Алгоритм интегрирования алгебраических функций (элементов алгебраического расширения поля рациональных функций от одной переменной) был сформулирован Дж. Дэвенпортом [ 6 ] в 1982 г. Этот алгоритм использует глубокие результаты алгебраической геометрии и весьма сложен для реализации. Дальнейшее развитие алгоритмы интегрирования в конечном виде получили в работах различных математиков, из которых следует отметить Б. Трейгера и М. Бронштейна. Основные направления исследований — повышение эффективности алгоритмов, расширение области их применения и исследование более широкого класса дифференциальных полей, чем поля элементарных функций.

Обобщением задачи интегрирования можно считать задачу нахождения в классе дифференциальных полей решений линейных дифференциальных уравнений с коэффициентами из дифференциального поля, принадлежащего классу 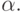Частный случай этой задачи для уравнения первого порядка приходится решать при интегрировании элементарных функций (в этом случае мы ищем решения в том же поле, в котором лежат коэффициенты исходного уравнения). Алгоритм нахождения решения в классе полей элементарных функций для уравнений второго порядка с коэффициентами из поля рациональных функций был предложен Ковасиком в 1978 году и вскоре был реализован в различных системах компьютерной алгебры. Обобщение алгоритма на уравнения произвольного порядка было получено М. Сингером. Сложность алгоритма Сингера очень высока, и трудно рассчитывать на его реализацию в обозримом будущем (есть реализация для дифференциальных уравнений 3-го порядка). Задачу о разрешимости линейного дифференциального уравнения в элементарных функциях можно разделить на два этапа. Вначале исследуется разрешимость уравнения в классе лиувиллевых функций (лиувиллевы функции получаются путем расширения исходного дифференциального поля последовательным присоединением элементов, являющихся либо алгебраическими, либо интегралами, либо экспонентами интегралов). Вопрос о разрешимости уравнения в лиувиллевых функциях решается дифференциальной теорией Галуа: линейное однородное дифференциальное уравнение разрешимо в лиувиллевых функциях тогда и только тогда, когда разрешима связная компонента его группы Галуа, являющейся линейной алгебраической группой. Далее задача сводится к уже рассмотренной задаче интегрирования. Рассмотрение задач, сформулированных в этом абзаце, выходит за рамки настоящего курса.

Компьютерная алгебра используется также при нахождении решений дифференциальных уравнений в виде степенных рядов, при анализе устойчивости решений, поиске периодических решений и в других задачах теории дифференциальных уравнений. Широко применяется компьютерная алгебра при построении разностных схем для численного решения дифференциальных уравнений.

1. Чем отличается компьютерная алгебра от вычислительной математики?
2. Какие типы чисел применяются в компьютерной алгебре?
3. Назовите несколько универсальных и специализированных систем компьютерной алгебры. Опишите область применения специализированных систем.
4. Сформулируйте проблему представления данных.
5. Для решения каких задач применяется алгоритм Евклида?
6. Для решения каких задач применяется метод Гаусса?
7. Какие задачи могут быть решены с использованием базисов Гребнера?
8. Для решения каких задач применяется алгоритм Кронекера?
9. Сформулируйте задачу интегрирования в конечном виде.
10. Назовите известные вам применения систем компьютерной алгебры.

Определения и обозначения

Следующие обозначения считаются фиксированными на протяжении всей книги:

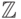• - кольцо целых чисел;
• Z_n — кольцо вычетов по модулю натурального числа n ;
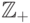• — множество неотрицательных целых чисел;
• — поле рациональных чисел;
• O_p — кольцо целых p -адических чисел;
• R_p — поле рациональных p -адических чисел;
• F — произвольное поле;
• F_q — конечное поле из q элементов;
• — поле вещественных чисел;
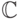• — поле комплексных чисел;
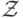• — кольцо гауссовых чисел (вида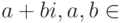 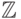i²=-1 );
• — поле рационально-комплексных чисел;
• - логическая переменная (типа "да/нет" ).

Запись алгоритмов осуществляем в форме, по возможности близкой к тем, которые используются в курсе информатики для средней школы и на механико-математическом факультете МГУ в курсе программирования [ 2 ] . Алгоритм снабжаем именем, за которым в скобках следует список параметров с указанием их типа. В записи алгоритмов // означает, что далее в строке следуют комментарии.

При необходимости вводим новые типы данных, в частности, для коммутативного кольца R с единицей введем типы "многочлен" и "разложение" следующим образом:

R[x] — многочлен:
	запись(степень: Z+
		коэффициенты: вектор элементов типа R
			с индексом 0..степень);
	разложение:
	запись(число_множителей: Z+
		множители: вектор элементов типа многочлен
			с индексом 1..число_множителей).