|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы вычисления размерностных многочленов
13.14. ЛЕММА. Пусть
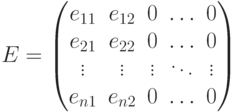
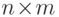 -матрица над
-матрица над 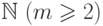 . Предположим, что
. Предположим, что  и
и 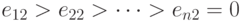 . Тогда
. Тогда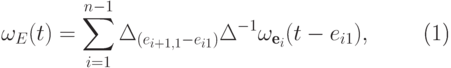 |
( 13.11) |
 .
.ДОКАЗАТЕЛЬСТВО.
Воспользуемся индукцией по  . Случай
. Случай 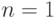 тривиален.
Пусть
тривиален.
Пусть 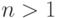 , и предположим, что утверждение леммы доказано для всех
матриц, число строк которых
меньше
, и предположим, что утверждение леммы доказано для всех
матриц, число строк которых
меньше  . Для доказательства соотношения (13.11)
для
. Для доказательства соотношения (13.11)
для 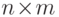 -матрицы
-матрицы 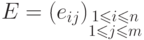 , у которой
, у которой 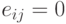
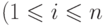 ,
, 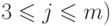 , прежде всего заметим, что
если
, прежде всего заметим, что
если 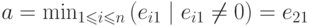 , то
, то
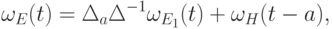
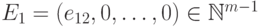 и
и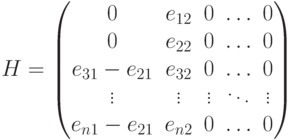
 является лишней, следовательно,
является лишней, следовательно,  , где
, где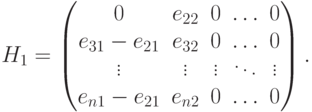
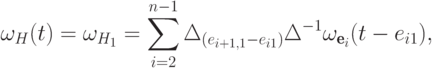
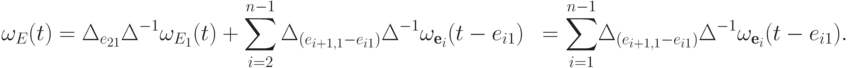
13.15. СЛЕДСТВИЕ. Пусть
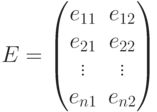
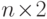 -матрица
над
-матрица
над 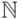 , такая, что
, такая, что  ,
, 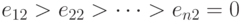 . Тогда
. Тогда 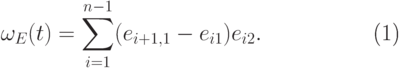 |
( 13.12) |
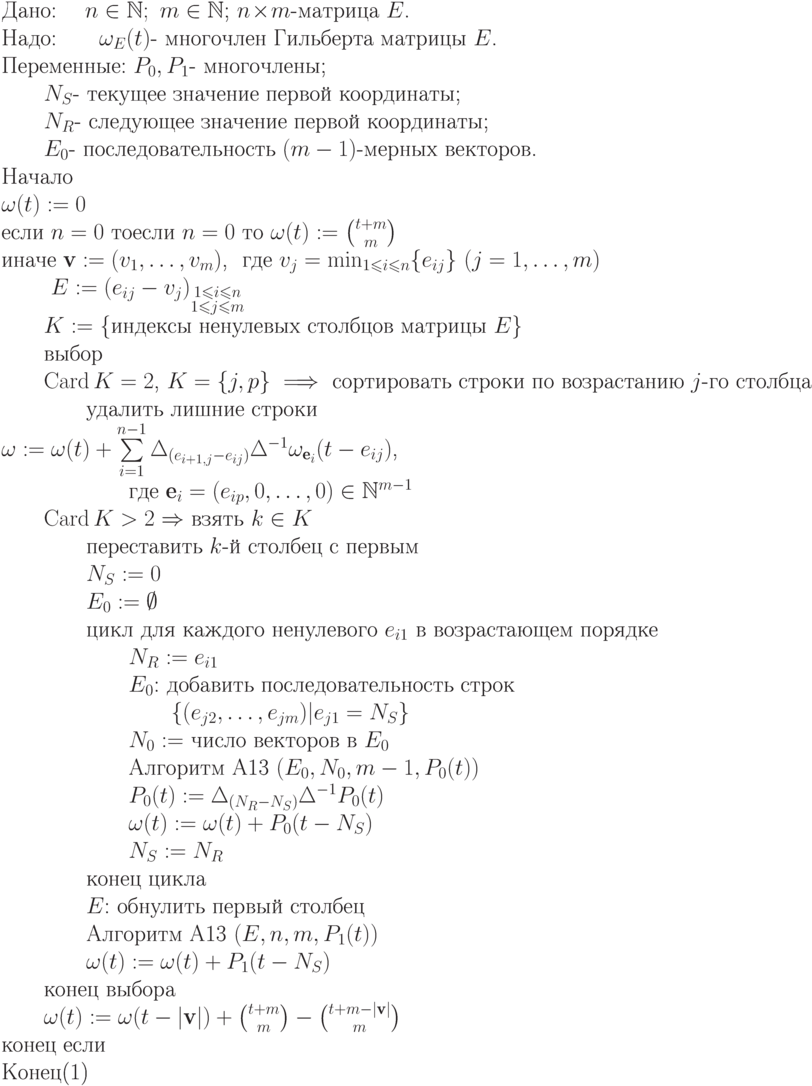
Приведенный здесь алгоритм A13
вычисления многочлена Гильберта  для
для 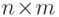 -матрицы
-матрицы  основан на данной выше схеме. В
соответствии с ней, воспользуемся (13.8), чтобы представить многочлен
основан на данной выше схеме. В
соответствии с ней, воспользуемся (13.8), чтобы представить многочлен  в виде суммы многочленов Гильберта матриц, которые
содержат менее
в виде суммы многочленов Гильберта матриц, которые
содержат менее  столбцов, и многочлена Гильберта
столбцов, и многочлена Гильберта 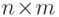 -матрицы
-матрицы 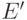 , содержащей
не более двух ненулевых столбцов (без потери общности можно считать, что
ненулевыми являются два первых столбца матрицы
, содержащей
не более двух ненулевых столбцов (без потери общности можно считать, что
ненулевыми являются два первых столбца матрицы 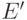 ). Многочлен
). Многочлен  вычисляется с помощью соотношения (13.10).
Сначала
переупорядочим строки так, чтобы элементы первого столбца удовлетворяли условию
леммы 13.14 (такое переупорядочение
требует
вычисляется с помощью соотношения (13.10).
Сначала
переупорядочим строки так, чтобы элементы первого столбца удовлетворяли условию
леммы 13.14 (такое переупорядочение
требует 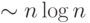 элементарных операций). Тогда видно, что если второй ненулевой столбец не
упорядочен в обратном порядке, то матрица
элементарных операций). Тогда видно, что если второй ненулевой столбец не
упорядочен в обратном порядке, то матрица  содержит лишние
строки (в
точности те строки
содержит лишние
строки (в
точности те строки  , в которых
, в которых 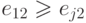 для
некоторого
для
некоторого 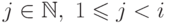 ). Таким образом, получаем
следующую оценку
числа
). Таким образом, получаем
следующую оценку
числа 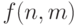 элементарных операций, которые требуются для
вычисления
многочлена Гильберта
элементарных операций, которые требуются для
вычисления
многочлена Гильберта  для
для 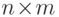 -матрицы
-матрицы  с помощью
алгоритма A13:
с помощью
алгоритма A13:
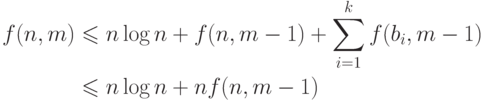
 ;
; 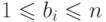
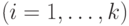 .
Следовательно, алгоритм A13 имеет асимптотическую
сложность
.
Следовательно, алгоритм A13 имеет асимптотическую
сложность 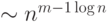 при
при 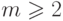 (если
(если 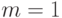 , то асимптотическая сложность
, то асимптотическая сложность 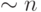 ).
).
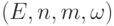 .
.