|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы вычисления размерностных многочленов
13.11. ПРИМЕР.
Вычислим многочлен
Гильберта  матрицы
матрицы
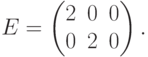
Сначала находим 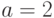 . Применяя (13.9),
получаем
. Применяя (13.9),
получаем

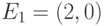 и
и 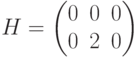 . Ясно, что
. Ясно, что 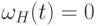 (см. теорему 12.8(6)) и
(см. теорему 12.8(6)) и 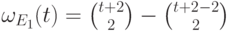 , следовательно, (см. 13.8)
, следовательно, (см. 13.8)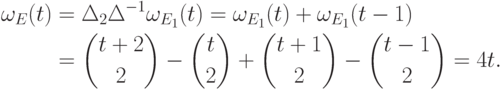
Заметим, что вычисление многочлена Гильберта  по
одному из алгоритмов A9, A10, A11 или A12 приводит к представлению этого многочлена в виде
по
одному из алгоритмов A9, A10, A11 или A12 приводит к представлению этого многочлена в виде 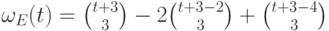 . Однако, применяя лемму 13.10, мы получаем
многочлен
. Однако, применяя лемму 13.10, мы получаем
многочлен  в виде суммы многочленов вида
в виде суммы многочленов вида 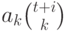
 ,
, 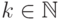 ,
,  . Максимальная степень этих многочленов меньше
степени многочленов, фигурирующих в подобном представлении
для
. Максимальная степень этих многочленов меньше
степени многочленов, фигурирующих в подобном представлении
для  , когда
, когда  вычисляется
по одному из алгоритмов A9, A10, A11 или A12.
вычисляется
по одному из алгоритмов A9, A10, A11 или A12.
Следующая лемма дает возможность оценивать степень многочлена Гильберта и вычислять его старший коэффициент, не вычисляя многочлен Гильберта полностью.
13.12. ЛЕММА. Пусть 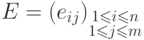 -
- 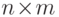 -матрица
над
-матрица
над 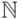 и
и  - неотрицательное
целое число. Тогда
- неотрицательное
целое число. Тогда  если и только если
для любого
подмножества
если и только если
для любого
подмножества  , состоящего
из
, состоящего
из 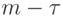 элементов множества
элементов множества 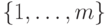 , существует строка
, существует строка  матрицы
матрицы  ,
такая, что все элементы этой строки,
стоящие в столбцах с индексами из
,
такая, что все элементы этой строки,
стоящие в столбцах с индексами из  , равны нулю. В
частности,
, равны нулю. В
частности, 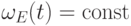 тогда и только тогда,
когда
тогда и только тогда,
когда  содержит диагональную
подматрицу.
содержит диагональную
подматрицу.
Доказательство леммы проводится индукцией по сумме элементов
матрицы  и оставляется читателю в качестве упражнения.
и оставляется читателю в качестве упражнения.
Матрицу  над
над 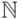 назовем нормализованной, если каждый столбец
матрицы
назовем нормализованной, если каждый столбец
матрицы  содержит нуль. Ниже будет показано, что
если
содержит нуль. Ниже будет показано, что
если  - нормализованная
- нормализованная 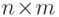 -матрица, то
алгоритм вычисления размерностного многочлена
-матрица, то
алгоритм вычисления размерностного многочлена  ,
основанный на лемме 13.10, требует
меньшего числа операций, чем для произвольной
,
основанный на лемме 13.10, требует
меньшего числа операций, чем для произвольной 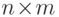 -матрицы.
В то же время, для сведения задачи вычисления размерностного многочлена
произвольной
-матрицы.
В то же время, для сведения задачи вычисления размерностного многочлена
произвольной 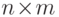 -матрицы над
-матрицы над 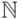 к аналогичной
задаче для нормализованной
к аналогичной
задаче для нормализованной 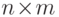 -матрицы можно
воспользоваться теоремой 12.8(9).
-матрицы можно
воспользоваться теоремой 12.8(9).
13.13. ЛЕММА. Пусть 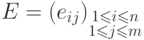 -
- 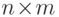 -матрица над
-матрица над 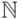 и предположим, что
и предположим, что 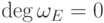 .
.
-
Если
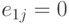 при
при 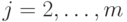 и
и 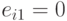 при
при 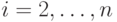 , то
, то 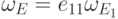 , где
, где 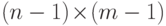 - матрица
- матрица 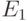 получена из
получена из  удалением первой строки и первого столбца.
удалением первой строки и первого столбца. -
Если матрица
 получена из
получена из  посредством обнуления
первого столбца, то
посредством обнуления
первого столбца, то 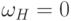 .
. -
Если
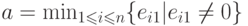 , тогде матрица
, тогде матрица
( 13.10) 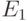 получена из
получена из  удалением первого столбца
и всех строк, содержащих ненулевые элементы в первом столбце, а
удалением первого столбца
и всех строк, содержащих ненулевые элементы в первом столбце, а  , где
, где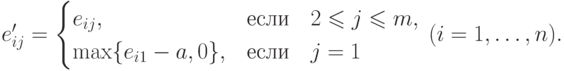
ДОКАЗАТЕЛЬСТВО.
(1) Если 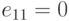 , то в
, то в  имеется нулевая строка,
следовательно,
имеется нулевая строка,
следовательно, 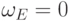 (см. теорему 12.8(6)).
Если
(см. теорему 12.8(6)).
Если  , то применяя (12.2)
к
, то применяя (12.2)
к  и
и 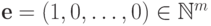 ,
получаем
,
получаем
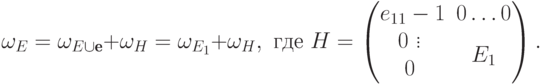
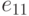 дает требуемый
результат.
дает требуемый
результат.(2) Лемма 13.12 утверждает,
что  содержит строку, в которой ненулевой может быть только первая
координата. Значит
содержит строку, в которой ненулевой может быть только первая
координата. Значит  содержит нулевую строку,
следовательно,
содержит нулевую строку,
следовательно, 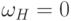 .
.
(3) Соотношение (13.10) следует из (12.2), записанного
для  и
и  .
.
Пользуясь леммой 13.13, можно
предложить следующий метод вычисления
многочлена Гильберта 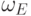 матрицы
матрицы  в случае,
когда
в случае,
когда 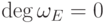 :
применить соотношение (13.10)
к
:
применить соотношение (13.10)
к 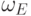 (где
(где  - минимальный
ненулевой элемент в первом столбце матрицы
- минимальный
ненулевой элемент в первом столбце матрицы  ), затем выписать
аналогичное
представление для
), затем выписать
аналогичное
представление для 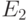 и т. д. После конечного числа таких шагов получим
представление многочлена
и т. д. После конечного числа таких шагов получим
представление многочлена 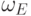 в виде суммы многочленов
Гильберта матриц
в виде суммы многочленов
Гильберта матриц 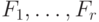
 ,
, 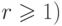 с
с  столбцами и многочлена
Гильберта
столбцами и многочлена
Гильберта 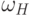 , где элементы
матрицы
, где элементы
матрицы  равны
равны
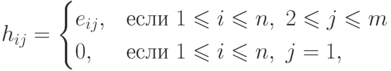
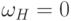 (см. лемму 13.13(2)). Применяя описанную
процедуру к каждой из матриц
(см. лемму 13.13(2)). Применяя описанную
процедуру к каждой из матриц 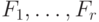 , мы сводим вычисление
многочлена
, мы сводим вычисление
многочлена 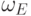 к вычислению многочленов Гильберта для
некоторых матриц с
к вычислению многочленов Гильберта для
некоторых матриц с  столбцами и т.д., пока не получим
матрицы, состоящие из единственного
столбца. Как мы знаем, многочлен Гильберта такой матрицы совпадает с ее
минимальным элементом.
столбцами и т.д., пока не получим
матрицы, состоящие из единственного
столбца. Как мы знаем, многочлен Гильберта такой матрицы совпадает с ее
минимальным элементом.В общем случае (без условия  ) вычисление
размерностного
многочлена
) вычисление
размерностного
многочлена  для
для 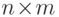 -матрицы
-матрицы 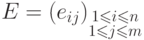 по описанной схеме
(используя (13.9) вместо (13.10)) можно свести к вычислению
размерностных многочленов матриц, число столбцов в которых
меньше
по описанной схеме
(используя (13.9) вместо (13.10)) можно свести к вычислению
размерностных многочленов матриц, число столбцов в которых
меньше  , и
размерностных многочленов некоторых
, и
размерностных многочленов некоторых 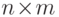 -матриц с нулевым
первым
столбцом. Более точно: если первый столбец матрицы
-матриц с нулевым
первым
столбцом. Более точно: если первый столбец матрицы  содержит
ненулевые
элементы, то мы полагаем
содержит
ненулевые
элементы, то мы полагаем 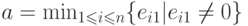 и
применяем (13.19). Затем применяем то же самое соотношение
к
и
применяем (13.19). Затем применяем то же самое соотношение
к  (см.
лемму 13.10) и т. д. В результате
получим разложение многочлена
(см.
лемму 13.10) и т. д. В результате
получим разложение многочлена  в сумму многочленов
вида
в сумму многочленов
вида  , где
, где  и
и 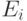 - либо матрица, число столбцов в которой
меньше
- либо матрица, число столбцов в которой
меньше  , либо
, либо 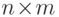 -матрица с нулевым первым столбцом. Для вычисления размерностных
многочленов
матриц второго типа применяем описанный метод ко второму столбцу и т. д., пока
не получим представление многочлена
-матрица с нулевым первым столбцом. Для вычисления размерностных
многочленов
матриц второго типа применяем описанный метод ко второму столбцу и т. д., пока
не получим представление многочлена  в виде суммы
размерностных
многочленов матриц, число столбцов в которых меньше
в виде суммы
размерностных
многочленов матриц, число столбцов в которых меньше  , и
размерностных
многочленов матриц с не более чем двумя ненулевыми столбцами. Размерностный
многочлен матрицы последнего типа может быть найден с помощью следующего
утверждения.
, и
размерностных
многочленов матриц с не более чем двумя ненулевыми столбцами. Размерностный
многочлен матрицы последнего типа может быть найден с помощью следующего
утверждения.
