НОУ ИНТУИТ | Введение в алгебру. Лекция 4: Кольцо многочленов от одной переменной

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5296 / 587 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 66 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Следствие 1.13.6. Пусть K - поле. $U(K[x])=K\setminus \{0\}$ (здесь U(R) - группа обратимых элементов кольца R ).

Доказательство. Если 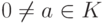$0\ne a\in K$ , то $a^{-1}\in K\subseteq K[x]$ , т. е. $a\in U(K[x])$ .

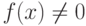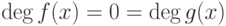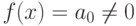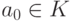Если f(x)g(x)= 1, то $f(x)\ne 0$ , $g(x)\ne 0$ , $\deg f(x)+\deg g(x)=0$ , и поэтому $\deg f(x)=0=\deg g(x)$ , т. е. $f(x)=a_0\ne 0$ , $a_0\in K$ .

Упражнение 1.13.7. (ax+b)(cx+d)=acx²+(ad+bc)x+bd, требующее четырех умножений ( ac, ad, bc, bd ) и одного сложения ( ad+bc ), может быть вычислено с помощью трех умножений и четырех сложений и вычитаний: 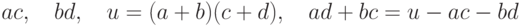$ac,\quad bd,\quad u=(a+b)(c+d),\quad ad+bc=u-ac-bd$ .

А. А. Карацуба использовал это соображение для построения быстрых алгоритмов умножения чисел и многочленов.

Теорема 1.13.8 (алгоритм деления с остатком в кольце многочленов). Для любых многочленов $f(x),g(x)\in K[x]$ , $g(x)\ne 0$ , существуют (и притом единственные) многочлены $q(x),r(x)\in K[x]$ такие, что:

f(x)=g(x)q(x)+r(x) ;
либо r(x)=0, либо $r(x)\ne 0$ , $\deg r(x)<\deg g(x)$ .

Доказательство-алгоритм (деление многочленов столбиком).

Пусть f(x) = a_nxⁿ+...+a₁x+a₀, g(x) = b_sx^s+...+b₁x+b₀, $b_s\ne 0$ .

Если n<s, то утверждение 1) очевидно:

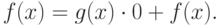
$f(x)=g(x)\cdot 0+f(x).$

Пусть $n\geq s$ . Тогда:

$\begin{fl} & f(x)-\frac{a_n}{b_s}x^{n-s}g(x)=f_1(x)= a_{1,n_1}x^{n_1}+..., & & s \leq n_1<n,\\ & f_1(x)-\frac{a_{1,n_1}}{b_s}x^{n_1-s}g(x)= \lefteqn{f_2(x)=a_{2,n_1}x^{n_2}+...,}\\[-\jot] & & & s \leq n_2<n_1,\\ & ...\\ & f_{k-2}(x)-\frac{a_{k-2,n_{k-2}}}{b_s}x^{n_{k-2}-s}g(x)= \lefteqn{f_{k-1}(x)=a_{k-1,n_{k-1}}x^{n_{k-1}}+...,} \\ & & & s \leq n_{k-1}<n_{k-2},\\ & f_{k-1}(x)-\frac{a_{k-1,n_{k-1}}}{b_s}x^{n_{k-1}-s}g(x)= \lefteqn{f_k(x)=a_{k,n_k}x^{n_k}+...,}\\* & & & \begin{cases} f_k(x)=0\text{ или}\\ n_k<\!s,\ n_k<n_{k-1}. \end{cases} \end{fl}$

Складывая все эти равенства и сокращая, получаем

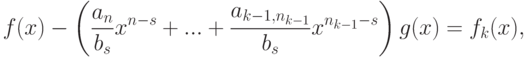
$f(x)-\left(\frac{a_n}{b_s}x^{n-s}+...+ \frac{a_{k-1,n_{k-1}}}{b_s}x^{n_{k-1}-s}\right)g(x)=f_k(x),$

т. е. f(x)=q(x)g(x)+r(x), где

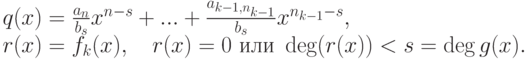
$\begin{ga} q(x)=\frac{a_n}{b_s}x^{n-s}+...+ \frac{a_{k-1,n_{k-1}}}{b_s}x^{n_{k-1}-s},\\ r(x)=f_k(x),\quad r(x)=0 \text{ или } \deg(r(x))<s=\deg g(x). \end{ga}$

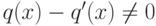Если f(x)=g(x)q(x)+r(x)=g(x)q'(x)+r'(x), при этом r(x),r'(x) или равны нулю, или имеют степень, меньшую чем $\deg g(x)=s$ , то g(x)(q(x)-q'(x))=r'(x)-r(x). Если $q(x)-q'(x)\ne 0$ , то получаем противоречие, поскольку степень левой части ${\ge}\,\deg g(x)$ , а многочлен в правой части или нулевой, или его степень ${<}\,\deg g(x)$ . Итак, q(x)=q'(x), и поэтому r'(x)=r(x).

Замечание 1.13.9. Если K - подполе поля K' (например, 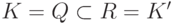$K=Q \subset R=K'$ ), $f(x),g(x)\in K[x]\subseteq K'[x]$ , f(x)=g(x)q(x)+r(x) - деление с остатком в кольце многочленов K'[x], то $q(x),r(x)\in K[x]$ .

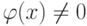Определение 1.13.10. Пусть $f(x),\varphi(x)\in K[x]$ , $\varphi(x)\ne 0$ . Будем говорить, что многочлен f(x) делится на 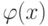$\varphi(x)$ , если 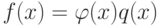$f(x)=\varphi(x)q(x)$ (т. е. остаток r(x) при делении на 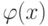$\varphi(x)$ равен нулю).

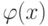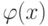Замечание 1.13.11. Совокупность $\varphi(x)K[x]=\{\varphi(x) f(x)\mid \allowbreak f(x)\in K[x]\}$ всех многочленов, делящихся на $\varphi(x)$ , является идеалом в кольце K[x] (называемым главным идеалом, порожденным $\varphi(x)$ ).

Упражнение 1.13.12. Пусть K - поле. Покажите, что кольцо многочленов K[x] является коммутативным кольцом главных идеалов.

Отметим ряд свойств делимости многочленов.

Лемма 1.13.13. Если f(x) делится на g(x), g(x) делится на h(x), то f(x) делится на h(x).

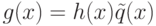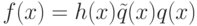Доказательство. Действительно, если f(x)=g(x)q(x), $g(x)=h(x)\tilde q(x)$ , то $f(x)=h(x)\tilde q(x)q(x)$ .

Лемма 1.13.14. Если f(x) и g(x) делятся на h(x), то f(x)+g(x), f(x)-g(x) делятся на h(x).

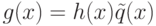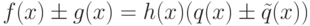Доказательство. Действительно, если f(x)=h(x)q(x), $g(x)=h(x)\tilde q(x)$ , то $f(x)\pm g(x)=h(x)(q(x)\pm\tilde q(x))$ .

Лемма 1.13.15. Если многочлен f(x) делится на h(x), $g(x)\in K[x]$ , то f(x)g(x) делится на h(x).

Доказательство. Действительно, если f(x)=h(x)q(x), то f(x)g(x)=h(x)(q(x)g(x)).

Лемма 1.13.16. Если f₁(x),...,f_k(x) делятся на h(x), $g_1(x),..., \allowbreak g_k(x)\in K[x]$ , то f₁(x)g₁(x)+...+f_k(x)g_k(x) делится на h(x).

Доказательство. Действительно, это вытекает из лемм 1.13.15 и 1.13.14.

Лемма 1.13.17. Если 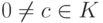$0\ne c\in K$ , то любой многочлен $f(x)\in K[x]$ делится на c.

Доказательство.Действительно, f(x)=c(c^-1f(x)).

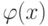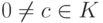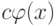Лемма 1.13.18. Если f(x) делится на $\varphi(x)$ и $0\ne c\in K$ , то f(x) делится на $c\varphi(x)$ .

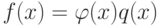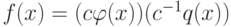Доказательство.Действительно, если $f(x)=\varphi(x)q(x)$ , то $f(x)=(c\varphi(x))(c^{-1}q(x))$ .

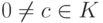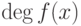Лемма 1.13.19. Многочлены вида cf(x), $0\ne c\in K$ , и только они являются делителями многочлена f(x), имеющими степень $\deg f(x)$ .

Лемма 1.13.20. Многочлен f(x) делится на g(x) и g(x) делится на f(x) тогда и только тогда, когда g(x)=cf(x), 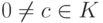$0\ne c\in K$ .

Лемма 1.13.21. Многочлены f(x) и cf(x), 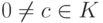$0\ne c\in K$ , обладают одинаковым запасом делителей в кольце K[x].

Дальше >>

Авторизоваться

Введение в алгебру

Кольцо многочленов от одной переменной

Вопросы и ответы