НОУ ИНТУИТ | Введение в алгебру. Лекция 2: Группы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 09.09.2007 | Доступ: свободный | Студентов: 5299 / 587 | Оценка: 4.35 / 3.78 | Длительность: 13:51:00

ISBN: 978-5-9556-0038-3

Тема: Математика

Специальности: Математик

Теги: beta, алгебра, алгоритмы, гомоморфизм групп, гомоморфизм группоидов, группоид, изоморфизм группоидов, инъекция, коэффициентами системы, моноид, полугруппа, расширенная матрица, старший коэффициент, элементы

|

Вам нравится? Нравится 66 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теорема 1.9.16. Пусть G - группа, $\{H_i\mid i\in I\}$ - любое семейство подгрупп группы G. Тогда их пересечение $H=\smash[b]{\bigcap\limits_{i\in I}H_i}$ также является подгруппой.

Доказательство.

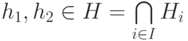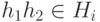Если $h_1,h_2\in H=\bigcap\limits_{i\in I}H_i$ , то $h_1,h_2\in H_i$ для каждого i. Так как H_i - подгруппа, то $h_1h_2\in H_i$ для каждого i, и поэтому $h_1h_2\in\bigcap\limits_{i\in I}H_i=H$ .
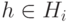Если $h\in H=\bigcap\limits_{i\in I}H_i$ , то $h\in H_i$ для каждого i. Так как H_i - подгруппа, то $h^{-1}\in H_i$ для каждого i, и поэтому $h^{-1}\in \smash[b]{\bigcap\limits_{i\in I}H_i}=H$ .

Итак, $H=\bigcap\limits_{i\in I}H_i$ - подгруппа группы G.

Примеры 1.9.17 (примеры подгрупп).

Четные числа 2Z - подгруппа в группе целых чисел (Z,+).
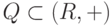$Z\subset (Q,{+})$ , $Q\subset(R,{+})$ , $R\subset (C,{+})$ - подгруппы.
В любой группе G имеем наименьшую подгруппу H={e} (и наибольшую подгруппу H=G ).

Задача 1.9.18. Группа, имеющая лишь конечное число подгрупп, конечна.

Пусть a - элемент группы G. Рассмотрим в G следующее подмножество: $(a)=\{a^n\mid n\in Z\}$ (т. е. совокупность всех целых степеней элемента a ).

Лемма 1.9.19.

является коммутативной подгруппой группы ;
(т. е. число элементов в подгруппе равно порядку элемента ).

Доказательство.

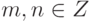
Для $m,n\in Z$ $a^ma^n=a^{m+n}\in (a);\quad (a^n)^{-1} = a^{-n}\in (a)$ . Таким образом, для (a) выполнены условия предыдущей леммы, т. е. $(a)=\{a^n\mid n\in Z\}$ - подгруппа группы G. Так как a^maⁿ=a^m+n=aⁿa^m, то (a) - коммутативная группа.
Если 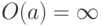$O(a)=\infty$ , то (a)={...,a^-1,e,a,...}, при этом в ряду целых степеней элемента a все элементы различны, т. е. $|(a)|=\infty$ . Если же $O(a)=n<\infty$ , то, как мы отметили ранее, (a)={e,a,...,a^n-1} и |(a)|=n=O(a)

Пример 1.9.20. Если G=Z и a=2, то $(a)=\{na\mid a\in Z\}=2Z$ (все четные числа).

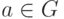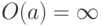Группа G называется циклической, если найдется такой элемент $a\in G$ , что (a)=G, т. е. все элементы группы G являются (целыми) степенями этого элемента a , называемого в этом случае циклическим образующим группы G. Если $O(a)=n<\infty$ , то G=(a) - циклическая группа из n элементов; если же $O(a)=\infty$ , то G=(a) - бесконечная (счетная!) циклическая группа.

Замечание 1.9.21. Любая циклическая группа G=(a) является конечной или счетной коммутативной группой. Поэтому любая некоммутативная группа не является циклической и любая несчетная группа не является циклической группой.

Примеры 1.9.22.

(Z,+)=(1)=(-1) (это показывает, что циклических образующих может быть много!).
Группа действительных чисел (R,+) не является счетной, поэтому она не является циклической.
Показать, что счетная группа (Q,+) рациональных чисел не является циклической.

Пусть G и G' - группы. Напомним, что отображение $f: G\to G'$ , для которого f(ab)=f(a)f(b) для всех элементов $a,b\in G$ , называется гомоморфизмом .

Пример 1.9.23. Пусть 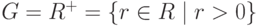$G=R^+=\{r\in R\mid r>0\}$ с операцией умножения, G'=(R,+) с операцией сложения. Так как для отображения $\ln: R^+\to R$ имеем $\ln(ab)=\ln(a)+\ln(b)$ для всех $a,b\in R^+$ , то $\ln$ - гомоморфизм групп.

Упражнение 1.9.24. Найти все гомоморфизмы $f: G\to G'$ , где G=(a), O(a)=m, G'=(b), O(b)=n (в частности, для m=12, n=15 ).

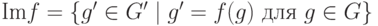Для гомоморфизмов $f: G\to G'$ определим: $\text{Im}f= \{g'\in G'\mid g'=f(g) \text{ для }g\in G\}$ образ гомоморфизма f ); $\text{Ker} f=\{g\in G\mid f(g)=e'\}$ , где e' - нейтральный элемент группы G' ядро гомоморфизма f ).

Упражнение 1.9.25. В рассмотренных выше примерах найти образ и ядро гомоморфизма.

Задача 1.9.26. Доказать, что не существует сюръективного гомоморфизма $(Q,{+})\to (Z,{+})$ .

Указание. В (Q,+) уравнение nx=a имеет (и единственное) решение для любых 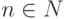$n\in N$ , $a\in Q$ .

Теорема 1.9.27 (свойства гомоморфизма групп). Пусть G и G' - группы, e и e' соответственно - их нейтральные элементы, $f: G\to G'$ - гомоморфизм групп. Тогда:

f(e)=e' ;
f(x^-1)=(f(x))^-1 для всех $x\in G$ ;
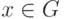H'= Im f - подгруппа группы G' ;
если G=(a) - циклическая группа, то Im f=(f(a)) также циклическая группа;
f(g^-1hg)=(f(g))^-1f(h)f(g) ;
Ker f - подгруппа группы G, при этом $g^{-1}(\text{Ker} f)g\subseteq \text{Ker} f$ для всех элементов $g\in G$ .

Доказательство.

Так как u=f(e)=f(e²)=f(e)f(e)=u², то u=e', т. е. f(e)=e'.
Так как f(x^-1)f(x)=f(x^-1x)=f(e)=e' и f(x)f(x^-1)=f(xx^-1)=f(e)=e', то f(x^-1)=(f(x))^-1.
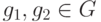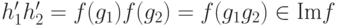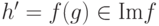Если h₁'=f(g₁) и h₂'=f(g₂) - элементы из $\text{Im} f$ , где $g_1,g_2\in G$ , то $h_1'h_2'=f(g_1)f(g_2)=f(g_1g_2)\in\text{Im} f$ . Если $h'=f(g)\in\text{Im} f$ , $g\in G$ , то $(h')^{-1}=(f(g))^{-1}=f(g^{-1})\in\text{Im} f$ . Итак, $\text{Im} f$ - подгруппа группы G'.
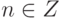Если G=(a) и $h'\in\text{Im} f$ , h'=f(g), $g\in G$ , то g=aⁿ, $n\in Z$ , и поэтому h'=f(g)=f(aⁿ)=(f(a))ⁿ. Итак, 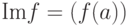$\text{Im} f=(f(a))$ - циклическая группа с образующим f(a).
следует из 2).
Если $h_1,h_2\in H=\text{Ker} f$ , то f(h₁)=e', f(h₂)=e'. Поэтому $f(h_1h_2)=f(h_1)f(h_2)=e'\cdot e'=e'$ , т. е. $h_1h_2\in\text{Ker} f$ .
Если $h\in\text{Ker} f$ , то f(h)=e', и поэтому f(h^-1)=(f(h))^-1=(e')^-1=e', т. е. $h^{-1}\in\text{Ker} f$ . Таким образом, Ker f - подгруппа группы G.

Если 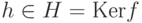$h\in H=\text{Ker} f$ , то f(h)=e'. Для любого элемента $g\in G$ имеем f(g^-1hg)=f(g^-1)f(h)f(g)=f(g)^-1e'f(g)=e'. Таким образом, $g^{-1}\text{Ker} fg\subseteq\text{Ker} f$ для всех элементов $g\in G$ .

Лемма 1.9.28. Если G, G', G'' - группы, 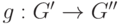$f: G\to G'$ , $g: G'\to G''$ - гомоморфизмы, то $gf: G\to G''$ - гомоморфизм.

Доказательство. Пусть $a,b\in G$ . Тогда (gf)(ab)=g[f(ab)]=g[f(a)f(b)]=[g(f(a))]\,[g(f(b))]=[(gf)(a)]\,[(gf)(b)].

Лемма 1.9.29. Пусть G, G' - группы, $f: G\to G'$ - гомоморфизм групп. Тогда:

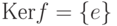f - инъекция в том и только в том случае, когда $\text{Ker} f=\{e\}$ ;
f - биекция в том и только в том случае, когда $\text{Ker} f =\{e\}$ , $\text{Im} f=G'$ .

Доказательство. Достаточно доказать 1). Если f - инъекция, то, учитывая равенство f(e)=e', видим, что 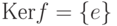$\text{Ker} f=\{e\}$ . Пусть теперь 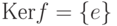$\text{Ker} f=\{e\}$ . Если f(a)=f(b) для $a,b\in G$ , то f(a^-1b)=f(a^-1)f(b)=[f(a)]^-1f(b)=e', т. е. $a^{-1}b\in\text{Ker} f=\{e\}$ . Поэтому a^-1b=e, т. е. a=b. Итак, f - инъекция.

Определение 1.9.30. Пусть G, G' - группы. Отображение $f: G\to G'$ назовем изоморфизмом групп, если:

f - гомоморфизм;
f - биекция.

Группы G и G' называются изоморфными если существует какой-либо изоморфизм $f: G\to G'$ (обозначение $G\cong G'$ ).,

Примеры 1.9.31. Следующие отображения - изоморфизмы групп:

$(R^+,{\cdot})=(\{r\in R\mid r>0\},{\cdot}) \overset{\ln}{\to} (R,{+})$ ;
$Z\to 2Z$ , $n\mapsto 2n$ .

Лемма 1.9.32. Если G, G', G'' - группы, 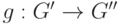$f: G\to G'$ , $g: G'\to G''$ - изоморфизмы, то gf и f^-1 - изоморфизмы (см. лемму 1.2.2).

Доказательство.

а) По лемме 1.9.29, gf - гомоморфизм. Так как gf и биекция, то gf - изоморфизм.

б) Мы знаем, что f^-1 - биекция. Пусть 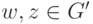$w,z\in G'$ . Тогда w=f(x), z=f(y), где $x,y\in G$ . Следовательно, wz=f(x)f(y)=f(xy). Поэтому f^-1(wz)=f^-1(f(xy))=xy=f^-1(w)f^-1(z), т. е. f^-1 - гомоморфизм. Итак, f^-1 - изоморфизм.

Следствие 1.9.33. Отношение $G\cong G'$ является отношением эквивалентности на классе групп.

Замечание 1.9.34. Изоморфные группы обладают одинаковыми "алгебраическими" свойствами.

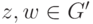Пример 1.9.35. Если группы G и G' изоморфны и G - коммутативная группа, то G' - также коммутативная группа. Действительно, пусть $f: G\to G'$ - некоторый изоморфизм. Если $z,w\in G'$ , то z=f(a), w=f(b) для некоторых $a,b\in G$ . Тогда zw=f(a)f(b)=f(ab)=f(ba)=f(b)f(a)=wz.

Дальше >>

Авторизоваться

Введение в алгебру

Группы

Вопросы и ответы