Реляционная модель данных
Специальные операции реляционной алгебры
Первой специальной операцией реляционной алгебры является горизонтальный выбор,или операция фильтрации,или операция ограничения отношений.Для определения этой операции нам необходимо ввести дополнительные обозначения.
Пусть а — булевское выражение, составленное из термов сравнения с помощью связок И ( 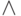 ), ИЛИ (
), ИЛИ ( 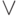 ), НЕ (
), НЕ ( 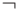 ) и, возможно, скобок. В качестве термов сравнения допускаются:
) и, возможно, скобок. В качестве термов сравнения допускаются:
-
терм А ос а,
где А — имя некоторого атрибута, принимающего значения из домена D ; a — константа, взятая из того же домена D,
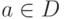 ; oc — одна из допустимых для данного домена D операций сравнения;
; oc — одна из допустимых для данного домена D операций сравнения; -
терм А ос В,
где А, В — имена некоторых
 -сравнимых атрибутов, то есть атрибутов, принимающих значения из одного и то же домена D.
-сравнимых атрибутов, то есть атрибутов, принимающих значения из одного и то же домена D.
Тогда результатом операции выбора, или фильтрации, заданной на отношении R в виде булевского выражения, определенного на атрибутах отношения R, называется отношение ![R[\alpha ]](/sites/default/files/tex_cache/8049712b795e8f30af27380737bff0f3.png) , включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации:
, включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации:
![R[\alpha (r)] = \{ r | r \in R \wedge \alpha (r) = "Истина"\}](/sites/default/files/tex_cache/97ced183a0bda841de42363642afb231.png)
Операция фильтрации является одной из основных при работе с реляционной моделью данных. Условие а может быть сколь угодно сложным.
Например, выбрать из R10 детали с шифром "0011003". R12 = R10 [ Шифр детали = "0011003"]
Следующей специальной операцией является операция проектирования.
Пусть R — отношение, SR = (A1, ... , An) — схема отношения R.
Обозначим через B подмножество [ Ai ] ; 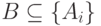 .
.
При этом пусть B1 — множество атрибутов из { Ai}, не вошедших в B.
Если B = {A1i, Ai2,..., Aik}, B = {A1, A2j ,..., Akj} и 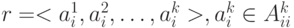 ,
,
то r [B], s = < a1j, a2j, ... , amj > ; 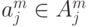 .
.
Проекцией отношения R на набор атрибутов В, обозначаемой R[B], называется отношение со схемой, соответствующей набору атрибутов В SR[B] = B, содержащему кортежи, получаемые из кортежей исходного отношения R путем удаления из них значений, не принадлежащих атрибутам из набора В.
R[B] = { r[B] }
По определению отношений все дублирующие кортежи удаляются из результирующего отношения.
Операция проектирования, называемая иногда также операцией вертикального выбора, позволяет получить только требуемые характеристики моделируемого объекта. Чаще всего операция проектирования употребляется как промежуточный шаг в операциях горизонтального выбора, или фильтрации. Кроме того, она используется самостоятельно на заключительном этапе получения ответа на запрос.
Например, выберем все цеха, которые изготавливают деталь "Болт М1".
Для этого нам необходимо из отношения R10 выбрать детали с заданным названием, а потом полученное отношение спроектировать на столбец "Цех". Результатом выполнения этих операций будет отношение R14:
R13 = R10 [ Название детали = "Болт М1" ] R14 = R13 [ Цех ]
Следующей специальной операцией реляционной алгебры является операция условного соединения.
В отличие от рассмотренных специальных операций реляционной алгебры: фильтрации и проектирования, которые являются унарными, то есть производятся над одним отношением, операция условного соединения является бинарной, то есть исходными для нее являются два отношения, а результатом — одно.
Пусть R = {r}, Q={q} - исходные отношения,
SR, SQ - схемы отношений R и Q соответственно.
SR = (A1, A2, ... , Ak) ; SQ = (B1, B2, ... , Bm), где Ai, Bj — имена атрибутов в схемах отношений R и Q соответственно. При этом полагаем, что заданы наборы атрибутов А и В
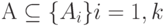 ;
; 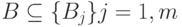
и эти наборы состоят из  -сравнимых атрибутов.
-сравнимых атрибутов.
Тогда соединением отношений R и Q при условии  будет подмножество декартова произведения отношений R и Q, кортежи которого удовлетворяют условию
будет подмножество декартова произведения отношений R и Q, кортежи которого удовлетворяют условию 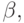 рассматриваемому как одновременное выполнение условий:
рассматриваемому как одновременное выполнение условий:
-
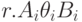 : i=1,k, где k — число атрибутов, входящих в наборы А и В, а
: i=1,k, где k — число атрибутов, входящих в наборы А и В, а 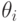 — конкретная операция сравнения.
— конкретная операция сравнения. -
 ;
; 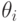 — i -й предикат сравнения, определяемый из множества допустимых на домене Di операций сравнения.
— i -й предикат сравнения, определяемый из множества допустимых на домене Di операций сравнения.![R [ \beta ] Q = \{ (r,q) | (r, q) | r.A \theta _{i} q.B_{i}= ";Истина"; i=1,k\}](/sites/default/files/tex_cache/c40ca3806902bddb95822020a232abad.png)
Например, рассмотрим следующий запрос. Пусть отношение R15 содержит перечень деталей с указанием материалов, из которых эти детали изготавливаются, и оно имеет вид:
| R15 | ||
|---|---|---|
| Шифр детали | Название детали | Материал |
| 00011073 | Гайка M1 | сталь-ст1 |
| 00011075 | Гайка М2 | сталь-ст2 |
| 00011076 | Гайка М3 | сталь-ст1 |
| 00011003 | Болт М1 | сталь-ст3 |
| 00011006 | Болт М3 | сталь-ст3 |
| 00013063 | Шайба М1 | сталь-ст1 |
| 00013066 | Шайба М3 | сталь-ст1 |
| 00011077 | Гайка М4 | сталь-ст2 |
| 00011004 | Болт М2 | сталь-ст3 |
| 00011005 | Болт М5 | сталь-ст3 |
| 00013062 | Шайба М2 | сталь-ст1 |
Получим перечень деталей, которые изготавливаются в цеху 1 из материала "сталь-ст1"
![R16 = (R15[(R15.Шифр \ детали =R_{10}.Шифр \ детали) \wedge R_{10}.Цех = "Цех1" \wedge R15.Материал ="сталь-ст1"] R_{10})[Название \ детали]](/sites/default/files/tex_cache/02dec935579b093f6a2558f278597fdb.png)
Последней операцией, включаемой в набор операций реляционной алгебры, является операция деления.
Для определения операции деления рассмотрим сначала понятие множества образов.
Пусть R — отношение со схемой SR = (A1, A2 ,..., Ak) ;
Пусть A — некоторый набор атрибутов 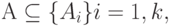 A1 — набор атрибутов, не входящих в множество A.
A1 — набор атрибутов, не входящих в множество A.
Пересечение множеств A и A1 пусто: 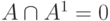 ; объединение множеств равно множеству всех атрибутов исходного отношения:
; объединение множеств равно множеству всех атрибутов исходного отношения: 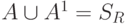 .
.
Тогда множеством образов элемента у проекции R[A] называется множество таких элементов y проекции R[A ], для которых сцепление (x, y) является кортежами отношения R, то есть
![QA(x) = \{ y | y \in R[A ] \wedge (x, y) \in R\}](/sites/default/files/tex_cache/b743b62e63e87066e864079ed8fd1710.png) - множество образов.
- множество образов.
Например, множеством образов отношения R15 по материалу "сталь-ст2" будет множество кортежей
R15.Материал = {< 00011075, Гайка М2, "сталь-ст2">, < 00011077, Гайка М4, "сталь-ст2">}
Дадим теперь определение операции деления.
Пусть даны два отношения R и T соответственно со схемами:
SR = (A1, A2, ... , Ak); ST = (B1, B2, ... , Bm) ;
A и B - наборы атрибутов этих отношений, одинаковой длины (без повторений);
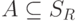 ;
; 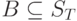 . Атрибуты A1 — это атрибуты из R, не вошедшие в множество A.
. Атрибуты A1 — это атрибуты из R, не вошедшие в множество A.
Пересечение множеств 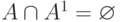 — пусто и
— пусто и 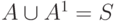 . Проекции R[A] и T[B] совместимы по объединению, то есть имеют эквивалентные схемы: SR[A] ~ ST[B] .
. Проекции R[A] и T[B] совместимы по объединению, то есть имеют эквивалентные схемы: SR[A] ~ ST[B] .
Тогда операция деления ставит в соответствие отношениям R и T отношение Q = R[A:B]T, кортежи которого являются теми элементами проекции R[A1], для которых T[B] входит в построенные для них множество образов:
![R[A:B]T = \{ r | r \in R[A^{1}] \wedge T[B] \subseteq \{ y | y \in R [A] \wedge (r, y) \in R \} \}](/sites/default/files/tex_cache/2c2a98c54693452f4a564110cd1d3a37.png) .
.
Операция деления удобна тогда, когда требуется сравнить некоторое множество характеристик отдельных атрибутов. Например, пусть у нас есть отношение R7, которое содержит номенклатуру всех выпускаемых деталей на нашем предприятии, а в отношении R10 хранятся сведения о том, что и в каких цехах действительно выпускается. Поставим задачу определить перечень цехов, в которых выпускается вся номенклатура деталей.
Тогда решением этой задачи будет операция деления отношения R10 на отношение R7 по набору атрибутов (Шифр детали, Наименование детали).
R 17 = R10[Шифр детали, Наименование детали: Шифр детали, Наименование детали]R7
Операция деления достаточно сложна для абстрактного представления. Она может быть заменена последовательностью других операций. Действительно, выполним тот же запрос с использованием других операций. Для этого определим последовательность промежуточных запросов, которая приведет нас к конечному результату:
- Построим отношение, которое моделирует ситуацию, когда в каждом цеху изготавливается вся номенклатура, это уже построенное нами ранее расширенное декартово произведение отношений R7 и R8. Это отношение R9:
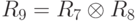
- Теперь найдем перечень того, что из обязательной номенклатуры не выпускается в некоторых цехах
R11= R9\R10
- Далее найдем те цеха, в которых не все детали выпускаются, для этого нам надо отношение R11 спроектировать на столбец "Цех":
R18 = R11[Цех]
- А теперь из перечня всех цехов вычтем те, кто выпускает не все детали, и получим ответ на запрос, и это будет тот же результат, что и в отношении R17.
Посмотрим, как работают операции реляционной алгебры для другого примера. Возьмем набор отношений, которые моделируют сдачу сессии студентами некоторого учебного заведения. Тема весьма понятная и привычная.
R1 = <ФИО, Дисциплина, Оценка> ; R2 = <ФИО, Группа> ; R3 = < Группы, Дисциплина>,
где R1 — информация о попытках (как успешных, так и неуспешных) сдачи экзаменов студентами; R2 — состав групп; R3 — список дисциплин, которые надо сдавать каждой группе. Домены для атрибутов формально задавать не будем, но, ориентируясь на здравый смысл, будем считать, что доменом для атрибута Дисциплина будет множество всех дисциплин, преподающихся в ВУЗе, доменом для атрибута Группа будет множество всех групп ВУЗа и т. д.
Покажем, каким образом можно получить из этих таблиц интересующие нас сведения с помощью реляционной алгебры. В каждом из приведенных примеров путем операций над исходными отношениями R1, R2, R3 формируются промежуточные отношения и результирующее отношение S, содержащее требуемую информацию.
- Список студентов, которые сдали экзамен по БД на "отлично". Результат может быть получен применением операции фильтрации по сложному условию к отношению R1 и последующим проектированием на атрибут "ФИО" (нам ведь требуется только список фамилий).
![S = (R_{1}[Оценка = 5 \wedge Дисциплина = "БД"])[ФИО]](/sites/default/files/tex_cache/2a5eb265e2a1680fd5da23eb5c4f6673.png) ;
; - Список тех, кто должен был сдавать экзамен по БД, но пока еще не сдавал. Сначала найдем всех, кто должен был сдавать экзамен по БД. В отношении R3 находится список всех дисциплин, по которым каждая группа должна была сдавать экзамены, ограничим перечень дисциплин только "БД". Для того чтобы получить список студентов, нам надо соединить отношение R3 с отношением R2, в котором определен список студентов каждой группы.
![R_{4} = (R_{2}[R_{3}.НомерГруппы = R_{2}.НомерГруппы \wedge R_{3}.Дисциплина = "БД"] R_{3})[ФИО]](/sites/default/files/tex_cache/a1b407c547872fcba3975dc37d7a80f1.png) ;
; - Теперь получим список всех, кто сдавал экзамен по "БД" (нас пока не интересует результат сдачи, а интересует сам факт попытки сдачи, то есть присутствие в отношении R1 ):
R5 = (R1 [Дисциплина = "БД"])[ФИО] ;
и, наконец, результат — все, кто есть в первом множестве, но не во втором:
S=R4 \R5 ;
- Список несчастных, имеющих несколько двоек:
![S = (R_{1}[R_{1}.ФИО = R'_{1}.ФИО \wedge R_{1}.Дисциплина \ne R'_{1}.Дисциплина \wedge R_{1}.Оценка < 2 \wedge R'_{1}.Оценка < 2] R'_{1})[ФИО]](/sites/default/files/tex_cache/ff2be006e680546b42b0d963ffe8e56b.png)
Этот пример весьма интересен: для поиска строк, удовлетворяющих в совокупности условию больше одного,применяется операция соединения отношения с самим собой. Поэтому мы как бы взяли копию отношения R1 и назвали ее R'1.
- Список круглых отличников. Строим список всех пар <студент—дисциплина>, которые в принципе должны быть сданы:
R4 = (R2[R2 Группа = R3.Группа] R3)[ФИО, Дисциплина] ;
Строим список пар <студент—дисциплина>, где получена оценка "отлично":
R5 = (R1[Оценка = 5])[ФИО, Дисциплина] ;
Строим список студентов, что-либо не сдавших на "отлично":
R6 = (R4 \ R5)[ФИО].
Наконец, исключив последнее отношение из общего списка студентов, получаем результат:
R2[ФИО] \ R6
Обратите внимание, что для получения множества студентов, что-либо не сдавших на "отлично" ( R6 ), мы осуществили "инверсию" множества всех отлично сданных пар <студент—дисциплина> ( R5 ) путем вычитания его из предварительного построенного универсального множества ( R4 ). Рекомендуем очень внимательно разобрать этот пример и вникнуть в смысл каждого действия — это очень пригодится для понимания реляционной алгебры.
